搜索
【题目】为了迎接杭州G20峰会，某校开展了设计“YJG20”图标的活动，下列图形中及时轴对称图形又是中心对称图形的是（ ）
A．
B．
C．
D．
参考答案：
【答案】D
【解析】
试题分析：根据轴对称图形与中心对称图形的概念求解．A、是轴对称图形．不是中心对称图形，因为找不到任何这样的一点，旋转180度后它的两部分能够重合；即不满足中心对称图形的定义．故错误；B、不是轴对称图形，因为找不到任何这样的一条直线，沿这条直线对折后它的两部分能够重合；即不满足轴对称图形的定义．也不是中心对称图形．故错误；C、不是轴对称图形，因为找不到任何这样的一条直线，沿这条直线对折后它的两部分能够重合；即不满足轴对称图形的定义．也不是中心对称图形．故错误；D、是轴对称图形，又是中心对称图形．故正确．
-
科目： 来源： 题型：
查看答案和解析>>【题目】正多边形的一个内角为140°，则该正多边形的边数为（ ）
A. 9 B. 8 C. 7 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（ ）
A．4 B．
C．3
D．2
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：若点P（a，b）在函数y=
的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的一个“派生函数”．例如：点（2， 
）在函数y=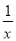
的图象上，则函数y=2x2+ 
称为函数y=
的一个“派生函数”．现给出以下两个命题：（1）存在函数y=
的一个“派生函数”，其图象的对称轴在y轴的右侧（2）函数y=
的所有“派生函数”的图象都经过同一点，下列判断正确的是（ ）A. 命题（1）与命题（2）都是真命题
B. 命题（1）与命题（2）都是假命题
C. 命题（1）是假命题，命题（2）是真命题
D. 命题（1）是真命题，命题（2）是假命题
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．
（1）k的值是 ；
（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=
图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若
=
，则b的值是 ．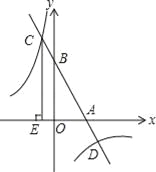
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学活动课上，某学习小组对有一内角为120°的平行四边形ABCD（∠BAD=120°）进行探究：将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转，且60°角的顶点始终与点C重合，较短的直角边和斜边所在的两直线分别交线段AB，AD于点E，F（不包括线段的端点）．
（1）初步尝试
如图1，若AD=AB，求证：①△BCE≌△ACF，②AE+AF=AC；
（2）类比发现
如图2，若AD=2AB，过点C作CH⊥AD于点H，求证：AE=2FH；
（3）深入探究
如图3，若AD=3AB，探究得：
的值为常数t，则t= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小强是一位密码翻译爱好者，在他的密码手册中，有这样一条信息：a﹣b，x﹣y，x+y，a+b，x2﹣y2 ， a2﹣b2分别对应下列六个字：北、爱、我、河、游、美，现将（x2﹣y2）a2﹣（x2﹣y2）b2因式分解，结果呈现的密码信息可能是（ ）
A.我爱美
B.河北游
C.爱我河北
D.美我河北
相关试题
