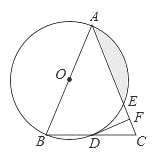
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
参考答案:
【答案】(1)见解析;(2)4π﹣8.
【解析】试题分析:(1)连接OD,易得∠ABC=∠ODB,由AB=AC,易得∠ABC=∠ACB,等量代换得∠ODB=∠ACB,利用平行线的判定得OD∥AC,由切线的性质得DF⊥OD,得出结论;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
试题解析:(1)连接OD,
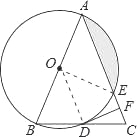
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵DF是⊙O的切线,
∴DF⊥OD,
∴DF⊥AC.
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE="8" ,
∴S阴影=4π-8.
-
科目: 来源: 题型:
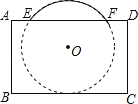
查看答案和解析>>【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据1,8,5,3,3的中位数是( )
A.3 B.3.5 C.4 D.5
-
科目: 来源: 题型:
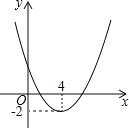
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图,则方程ax2+bx+c=m有实数根的条件是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8cm,点C是直线AB上一点,线段BC=3cm,D、E分别是线段AB与线段CB的中点,求线段DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅美丽的图案,在其顶点处由四个正多边形镶嵌而成,其中三个分别为正三角形、正四边形、正六边形,则另一个为()
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图有A、B、C、D、E五个居民点,每天产生的垃圾量(单位:吨),交通状况和每相邻两个居民点的距离如图所示,现要建一座垃圾中转站(只能建在A、B、C、D、E的其中一处),这五个居民点的垃圾都运到此中转站,那么中转站建在何处,才能使总的运输量最小?(圆圈内的数字为垃圾量,线段上的字母表示距离,b<a<c).中转站应建在 处.

相关试题

