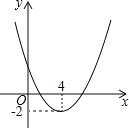
【题目】二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的图象如图,则方程ax2+bx+c=m有实数根的条件是 .
参考答案:
【答案】m≥﹣2
【解析】
试题分析:由于抛物线y=ax2+bx+c与直线y=m有交点时,方程ax2+bx+c=m有实数根,观察函数图象得到当m≥﹣2时,抛物线y=ax2+bx+c与直线y=m有交点,从而得到方程ax2+bx+c=m有实数根的条件.
解:当抛物线y=ax2+bx+c与直线y=m有交点时,方程ax2+bx+c=m有实数根,
因为直线y=﹣2与抛物线y=ax2+bx+c只有一个公共点,
所以当m≥﹣2时,抛物线y=ax2+bx+c与直线y=m有交点,
即方程ax2+bx+c=m有实数根的条件是m≥﹣2.
故答案为m≥﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( )
A.过马路的斑马线是平行线
B.100米跑道的跑道线是平行线
C.若a∥b,b∥d,则a⊥d
D.过直线外一点有且只有一条直线与已知直线平行
-
科目: 来源: 题型:
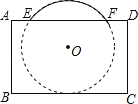
查看答案和解析>>【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据1,8,5,3,3的中位数是( )
A.3 B.3.5 C.4 D.5
-
科目: 来源: 题型:
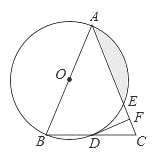
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB=8cm,点C是直线AB上一点,线段BC=3cm,D、E分别是线段AB与线段CB的中点,求线段DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅美丽的图案,在其顶点处由四个正多边形镶嵌而成,其中三个分别为正三角形、正四边形、正六边形,则另一个为()
A. 正三角形 B. 正四边形 C. 正五边形 D. 正六边形
相关试题

