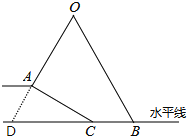
【题目】小明坐于堤边垂钓,如图,河堤AC的坡角为30°,AC长2![]() ,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
,钓竿AO的倾斜角∠ODC是60°,其长OA为5米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
参考答案:
【答案】浮漂B与河堤下端C之间的距离为3米.
【解析】
试题分析:先根据三角形内角和定理求出∠CAD=180°﹣∠ODB﹣∠ACD=90°,解Rt△ACD,得出AD=ACtan∠ACD=2米,CD=2AD=3米,再证明△BOD是等边三角形,得到BD=OD=OA+AD=7米,然后根据BC=BD﹣CD即可求出浮漂B与河堤下端C之间的距离.
解:∵AO的倾斜角是60°,
∴∠ODB=60°.
∵∠ACD=30°,
∴∠CAD=180°﹣∠ODB﹣∠ACD=90°.
在Rt△ACD中,AD=ACtan∠ACD=2![]() ×
×![]() =2(米),
=2(米),
∴CD=2AD=4米,
又∵∠O=60°,
∴△BOD是等边三角形,
∴BD=OD=OA+AD=2+5=7(米),
∴BC=BD﹣CD=7﹣4=3(米).
答:浮漂B与河堤下端C之间的距离为3米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形两边长分别是2 cm和5 cm,则这个三角形周长是( )
A. 9 cm B. 12 cm C. 9 cm或12 cm D. 14 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】肥皂泡的泡壁厚度大约是0.0007mm,0.0007用科学记数法表示为( )
A. 0.7×10﹣3 B. 7×10﹣3 C. 7×10﹣4 D. 7×10﹣5
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列等式错误的是( )
A. (2mn)2=4m2n2 B. (﹣2mn)2=4m2n2
C. (2m2n2)3=8m6n6 D. (﹣2m2n2)3=﹣8m5n5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )

A.8≤a≤15 B.5≤a≤8 C.7≤a≤8 D.7≤a≤15
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
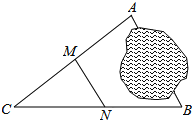
A.MN∥AB
B.AB=24m
C.△CMN∽△CAB
D.△CMN与四边形ABMN的面积之比为1:2
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,AB=4,BC=3,以点D为圆心作圆,使A、B、C三点中至少有一点在圆内且至少一点在圆外,⊙O的的半径r的取值范围是_________________
相关试题

