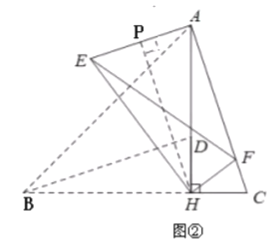
【题目】如图①,△ABC中,∠ABC=45°,AH⊥BC 于H,点D在AH上,且DH=CH,连结BD.将△BHD绕点H旋转,得到△EHF(点B,D分别与点E,F对应),连接AE.如图②,当点F落在AC上时(F不与C重合),若BC=4,tan∠ACH=3,则AE=_____.

参考答案:
【答案】![]()
![]()
![]()
![]()
【解析】在Rt△AHC中,由tan∠ACH=3,可得![]() =3, 设CH=x,则BH=AH=3x,由BC=4, 可得 3x+x=4, 解得 x=1.即可得AH=3, CH=1. 由旋转知:∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH. 所以∠EHA=∠FHC,
=3, 设CH=x,则BH=AH=3x,由BC=4, 可得 3x+x=4, 解得 x=1.即可得AH=3, CH=1. 由旋转知:∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH. 所以∠EHA=∠FHC, ![]() =1,即可判定△EHA∽△FHC,所以∠EAH=∠C,即可得tan∠EAH=tanC=3 ,如图②,过点H作HP⊥AE于P,则HP=3AP,AE=2AP. 在Rt△AHP中,AP2+HP2= AH2,∴AP2+(3AP)2= 9,解得AP=
=1,即可判定△EHA∽△FHC,所以∠EAH=∠C,即可得tan∠EAH=tanC=3 ,如图②,过点H作HP⊥AE于P,则HP=3AP,AE=2AP. 在Rt△AHP中,AP2+HP2= AH2,∴AP2+(3AP)2= 9,解得AP=![]() ,所以AE=
,所以AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课
A
B
C
D
E
F
人数
40
60
100
根据图表提供的信息,下列结论错误的是( )
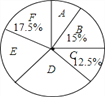
A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80,70
D. 喜欢选修课C的人数最少
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某一城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天,乙队单独完成这项工程需要90天;若由甲队先做20天,剩下的工程由甲、乙两队合做完成.
(1)甲、乙两队合作多少天?
(2)甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“任意打开我们的九上数学书,正好是第60页”,这是____(选填“随机”或“必然”)事件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
⑴若△ABC关于x轴对称的图形是△A1B1C1,直接写出A1、B1、C1的坐标;
⑵将△ABC绕点O按顺时针方向旋转90°得到△A2B2C2,画出△A2B2C2,并写出点A的对称点A2的坐标;
⑶计算△OA1A2的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:从第一本按标价的80%卖.
(1)小明要买20本时,到哪个商店较省钱?
(2)买多少本时给两个商店付相等的钱?
(3)小明现有40元钱,最多可买多少本?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP,BP.

(1)求证:四边形BMNP是平行四边形;
(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.
相关试题

