【题目】学校准备在校园内修建一个矩形的绿化带,矩形的面积为定值,它的一边 y与另一边 x之间的函数关系式如下图所示.
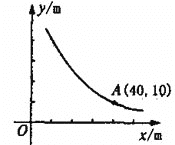
(1)绿化带面积是多少?你能写出这一函数表达式吗?
(2)完成下表,并回答问题:如果该绿化带的长不得超过40m,那么它的宽应控制在什么范围内?
![]()
参考答案:
【答案】(1)400(m 2),函数表达式为 y=![]() ;(2)40,20,
;(2)40,20, ![]() ,10,从图中可以看出.若长不超过40m,则它的宽应大于等于10m.
,10,从图中可以看出.若长不超过40m,则它的宽应大于等于10m.
【解析】试题分析:
(1)由“矩形的长=面积÷宽”可得: ![]() ,把点A(40,10)代入
,把点A(40,10)代入![]() 即可求出S和函数关系式;
即可求出S和函数关系式;
(2)根据(1)中所得函数关系式即可计算出表格中与![]() 对应的
对应的![]() 的值,由计算结果即可得到所求结论;
的值,由计算结果即可得到所求结论;
试题解析:
(1)设矩形面积为S,由题意可得: ![]() ,
,
把点A(40,10)代入![]() 可得:
可得: ![]() ,
,
∴矩形的面积S=400,函数关系式为: ![]() ;
;
(2)由![]() 计算完成表中数据如下:
计算完成表中数据如下:
| 10 | 20 | 30 | 40 |
| 40 | 20 |
| 10 |
由表中数据可知,若矩形长不超过40m,则矩形的宽不少于10m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )

A.96B.48C.60D.30
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆柱的底面半径是2cm,当圆柱的高h(cm)由大到小变化时,圆柱的体积V(cm3)随之发生变化。
(1)在这个变化过程中,自变量和因变量各是什么?
(2)在这个变化过程中,写出圆柱的体积为V与高h之间的关系式?
(3)当h由5cm变化到10cm时,V是怎样变化的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个图案都由若干个“●”组成,其中第①个图案中有7个“●”,第②个图案中有13个“●”,…,则第⑨个图案中“●”的个数为( )

A.87B.91C.103D.111
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
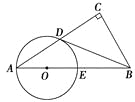
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
-
科目: 来源: 题型:
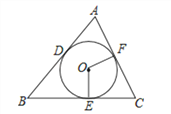
查看答案和解析>>【题目】如图,已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,S△ABC=10cm2,C△ABC=10cm且∠C=60°.求:
(1)⊙O的半径r;
(2)扇形OEF的面积(结果保留π);
(3)扇形OEF的周长(结果保留π)
相关试题

