【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
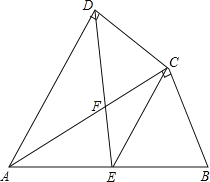
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求![]() 的值.
的值.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
试题分析:(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;
(2)由E为AB的中点,根据在直角三角形中,斜边上的中线等于斜边的一半,即可证得CE=![]() AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
AB=AE,继而可证得∠DAC=∠ECA,得到CE∥AD;
(3)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=ABAD;
(2)证明:∵E为AB的中点,
∴CE=![]() AB=AE,
AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)解:∵CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=![]() AB,
AB,
∴CE=![]() ×6=3,
×6=3,
∵AD=4,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在二元一次方程x+3y=8的解中,当x=2时,对应的y的值是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长分别为4,8,a,则a的取值范围是 ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( ).
A.4m﹣m=3 B.2m2m3=2m5
C.(﹣m3)2=m9 D.﹣(m+2n)=﹣m+2n
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,错误的有( )
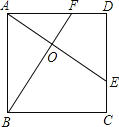
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数
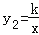 (k为常数,k≠0)的图象相交点A(1,3).
(k为常数,k≠0)的图象相交点A(1,3).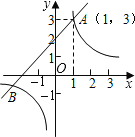
(1)求这两个函数的解析式及其图象的另一交点B的坐标;
(2)观察图象,写出使函数值y1≥y2的自变量x的取值范围.
相关试题

