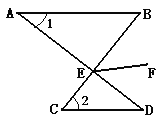
【题目】如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=300,∠2=400。(1)求∠B、∠D的度数.(2)求∠BEF的度数
参考答案:
【答案】(1)∠B=40°, ∠D=30°;(2)35°
【解析】
(1)根据平行线的性质,即可解答
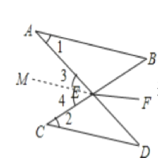
(2)首先过点E作EM∥AB,由AB∥CD,可得EM∥AB∥CD,然后根据两直线平行,内错角相等,即可求得∠AEC的度数,又由对顶角相等,求得∠BED的度数,由EF是∠BED的平分线,即可求得答案
(1)∵AB∥CD,∠1=30°,∠2=40°,
∴∠B=∠2,∠D=∠1(两直线平行,内错角相等)
∴∠B=40°, ∠D=30°;
(2)过点E作EM∥AB,
∵AB∥CD,
∴EM∥AB∥CD,
∵∠1=30°,∠2=40°,
∴∠3=∠1=30°,∠4=∠2=40°,
∴∠BED=∠AEC=∠3+∠4=70°,
∵EF是∠BED的平分线,
∴∠BEF=![]() ∠BED=
∠BED=![]() ×70°=35°
×70°=35°
故答案为:35°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90,AC=BC=2,E、F为线段AB上两动点,且∠ECF=45°,过点E、F分别作BC、AC的垂线相交于点D,垂足分别为H、G.现有以下结论:①当点E与点B重合时,DH=1;②GF+EH=EF;③AF2+BE2=EF2;④DGDH=2,其中正确结论为( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线AB与CD相交于点O,OE、OF分别是∠BOD、∠AOD的平分线。
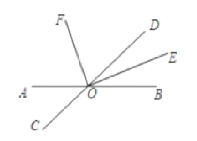
(1)∠DOE的补角是___;
(2)若∠BOD=62°,求∠AOE和∠DOF的度数;
(3)判断射线OE与OF之间有怎样的位置关系?并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D、E分别在钱段AB、AC上,CD与BE交于O,已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD

A. ∠B=∠CB. AD=AEC. BE=CDD. BD=CE
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(x―3)2=(3x+1)2 (2)x2-8x=-12
(3)3x2-4x-1=0(用配方法) (4)5x2―7x+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为
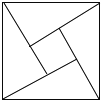
A. 3B. 4C. 5D. 8
相关试题

