【题目】如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合).
初步探究
(1)写出点B的坐标 ;
(2)点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;并求出这个图形所对应的函数表达式.
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.

参考答案:
【答案】(1)(![]() ,1);(2)证明见解析;(3)点P在过点B且与AB垂直的直线上,点P所在直线的函数表达式为y=
,1);(2)证明见解析;(3)点P在过点B且与AB垂直的直线上,点P所在直线的函数表达式为y=![]() x﹣2;(4)(﹣2
x﹣2;(4)(﹣2![]() ,0)或(﹣
,0)或(﹣![]() ,0)或(﹣2,0)或(2,0).
,0)或(﹣2,0)或(2,0).
【解析】
(1)如图1中,作BH⊥OA于H.利用等边三角形的性质,解直角三角形求出BH、OH即可;
(2)根据SAS即可判断;
(3)点P在过点B且与AB垂直的直线上.当点P在y轴上时,得P(0,﹣2).由B(![]() ,1).设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入即可解决问题;
,1).设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入即可解决问题;
(4)分四种情形分别求解即可解决问题;
(1)如图1中,作BH⊥OA于H.

∵△AOB是等边三角形,OA=OB=AB=2,∠BOH=60°
在Rt△OBH中,BH=OBsin60°=![]() ,OH=AH=1,
,OH=AH=1,
∴B(![]() ,1).
,1).
(2)如图2中

∵△AOB与△ACP都是等边三角形,
∴AO=AB,AC=AP,∠CAP=∠OAB=60°,
∴∠CAP+∠PAO=∠OAB+∠PAO,
即∠CAO=∠PAB,
在△AOC与△ABP中,

∴△AOC≌△ABP(SAS).
(3)如图2中,∵△AOC≌△ABP(SAS).
∴∠ABP=∠AOC=90°,
∴PB⊥AB,
∴点P在过点B且与AB垂直的直线上.
当点P在y轴上时,得P(0,﹣2).
∵B(![]() ,1).
,1).
设点P所在直线的函数表达式为:y=kx+b(k≠0).把点B、P的坐标分别代入,得
![]()
所以点P所在直线的函数表达式为:y=![]() x﹣2.
x﹣2.
(4)如图3中,

①当OB=BP1=2时,OC1=BP1=2,此时C1(2,0).
②当P2O=P2B时,OC2=BP2=![]() ,此时C2(﹣
,此时C2(﹣![]() ,0).
,0).
③当OB=BP3=2时,OC3
④当OB=OP4时,OC4=BP4=2![]() ,此时C4(﹣2
,此时C4(﹣2![]() ,0),
,0),
故答案为(﹣2![]() ,0)或(﹣
,0)或(﹣![]()
![]() ,0)或(﹣2,0)或(2,0).
,0)或(﹣2,0)或(2,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为(-1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>3.其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的中线,点
的中线,点 在
在 的延长线上的点,连接
的延长线上的点,连接 ,且
,且 ,过点
,过点 作
作 于点
于点 ,连接
,连接 ,若
,若 ,则
,则 的长为________________.
的长为________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )

A. 1 B. ﹣1 C. 2 D. ﹣2
-
科目: 来源: 题型:
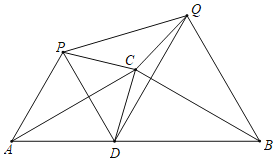
查看答案和解析>>【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ.
(1)证明:CP=CQ;
(2)求∠PCQ的度数;
(3)当点D是AB中点时,请直接写出△PDQ是何种三角形.
-
科目: 来源: 题型:
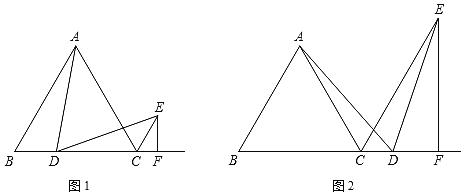
查看答案和解析>>【题目】在等边△ABC中,D为射线BC上一点,CE是∠ACB外角的平分线,∠ADE=60°,EF⊥BC于F.
(1)如图1,若点D在线段BC上,证明:∠BAD=∠EDC;
(2)如图1,若点D在线段BC上,证明:①AD=DE;②BC=DC+2CF(提示:构造全等三角形);
(3)如图2,若点D在线段BC的延长线上,直接写出BC、DC、CF三条线段之间的数量关系.
-
科目: 来源: 题型:
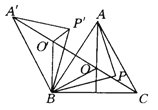
查看答案和解析>>【题目】如图所示,O是锐角三角形ABC内一点,∠AOB=∠BOC=∠COA=120°,P是△ABC内不同于O的另一点,△A′BO′、△A′BP′分别由△AOB、△APB旋转而得,旋转角都为60°,则下列结论中正确的有( ).(提示:有一个角是60°的等腰三角形是等边三角形)
①△O′BO为等边三角形,且A′、O′、O、C在一条直线上.
②A′O′+O′O=AO+BO. ③A′P′+P′P=PA+PB.
④PA+PB+PC>AO+BO+CO.
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

