搜索
【题目】如图，
为
的中线，点
在
的延长线上的点，连接
，且
，过点
作
于点
，连接
，若
，则
的长为________________.
参考答案：
【答案】3
【解析】
过点A作AF⊥EF于点F，通过证明△AFD≌△BHD（AAS），Rt△CAF≌ Rt△EBH（HL），得到BH= HD+DF=2DH，又因为 
为
的中线，
，所以S△BHD=
S△BHA=×18=9=×HD·HB=×HD·2HD，从而求解.
解：如图：过点A作AF⊥EF于点F，
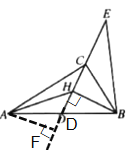
∵为的中线，，
∴AD=BD， ∠AFD=∠BHD=90°，
又∵∠ADF=∠BDH，
∴△AFD≌△BHD（AAS），
∴AF=BH，FD=HD，
∵在Rt△CAF和 Rt△EBH中，
∴Rt△CAF≌ Rt△EBH（HL）
∴EH=CF，
∴EH-CH=CF-CH，即EC=HF
∵BH=EC，EC=HF=HD+DF，HD=DF
∴BH= HD+DF=2DH,
∵为的中线，，
∴S△BHD=S△BHA=×18=9=×HD·HB=×HD·2HD,
解得：HD=3.
故答案为：3.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，△ABC是等边三角形，点D、E分别是边BC、CA上的点，且BD=CE，AD、BE相交于点O．
（1）求证：△BAE≌△ACD；
（2）求∠AOB的度数．
-
科目： 来源： 题型：
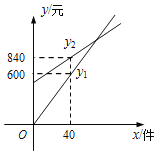
查看答案和解析>>【题目】某化妆品公司每月付给销售人员的工资有两种方案．方案一：没有底薪，只拿销售提成；方案二：底薪加销售提成．设x（件）是销售商品的数量，y（元）是销售人员的月工资．如图所示，y1为方案一的函数图象，y2为方案二的函数图象．已知每件商品的销售提成方案二比方案一少8元．从图中信息解答如下问题（注：销售提成是指从销售每件商品得到的销售额中提取一定数量的费用）：
（1）求y1的函数解析式；
（2）请问方案二中每月付给销售人员的底薪是多少元？
（3）小丽应选择哪种销售方案，才能使月工资更多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c(a≠0)的图像与x轴交于A、B两点，与y轴交于C点，且对称轴为直线x=1，点B坐标为(－1，0)．则下面的四个结论：①2a+b=0；②4a－2b+c＜0；③ac＞0；④当y＜0时，x＜－1或x＞3．其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C1，它与x轴交于两点O，A1；将C1绕A1旋转180°得到C2，交x轴于A2；将C2绕A2旋转180°得到C3，交x轴于A3；…如此进行下去，得到Cn，若点P（2017，m）在抛物线Cn上，则m为（ ）
A. 1 B. ﹣1 C. 2 D. ﹣2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点A的坐标是（0，2），点C是x轴上的一个动点．当点C在x轴上移动时，始终保持△ACP是等边三角形（点A、C、P按逆时针方向排列）；当点C移动到点O时，得到等边三角形AOB（此时点P与点B重合）．
初步探究
(1)写出点B的坐标 ；
(2)点C在x轴上移动过程中，当等边三角形ACP的顶点P在第三象限时，连接BP，求证：△AOC≌△ABP．
深入探究
(3)当点C在x轴上移动时，点P也随之运动．探究点P在怎样的图形上运动，请直接写出结论；并求出这个图形所对应的函数表达式．
拓展应用
(4)点C在x轴上移动过程中，当△POB为等腰三角形时，直接写出此时点C的坐标．
-
科目： 来源： 题型：
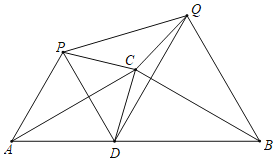
查看答案和解析>>【题目】如图，等腰△ABC中，CA=CB=4，∠ACB=120°，点D在线段AB上运动（不与A、B重合），将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ．
（1）证明：CP=CQ；
（2）求∠PCQ的度数；
（3）当点D是AB中点时，请直接写出△PDQ是何种三角形．
相关试题
