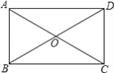
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F,M,N分别为OA,OB,OC,OD的中点,连接EF,FM,MN,NE.
(1)依题意,补全图形;
(2)求证:四边形EFMN是矩形;
(3)连接DM,若DM⊥AC于点M,ON=3,求矩形ABCD的面积.
参考答案:
【答案】(1)补图见解析;(2)证明见解析;(3) 36![]()
【解析】试题分析:(1)见图形;(2)根据三角形的中位线定理,先证四边形EFMN是平行四边形,再通过对角线相等证明四边形EFMN是矩形;(3)证△OCD是等边三角形。
试题解析:(1)解:如图所示:
(2)证明:∵点E,F分别为OA,OB的中点,∴EF∥AB,EF=![]() AB,
AB,
同理:NM∥CD,MN=![]() DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
DC,∵四边形ABCD是矩形,∴AB∥DC,AB=DC,AC=BD,
∴EF∥NM,EF=MN,∴四边形EFMN是平行四边形,
∵点E,F,M,N分别为OA,OB,OC,OD的中点,∴EO=![]() AO,MO=
AO,MO=![]() CO,
CO,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,∴EM=EO+MO=
BD,∴EM=EO+MO=![]() AC,
AC,
 同理可证FN=
同理可证FN=![]() BD,∴EM=FN,∴四边形EFMN是矩形.
BD,∴EM=FN,∴四边形EFMN是矩形.
(3)解:∵DM⊥AC于点M,由(2)MO=![]() CO,∴DO=CD,
CO,∴DO=CD,
在矩形ABCD中,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD,AC=BD,
BD,AC=BD,
∴AO=BO=CO=DO,∴△COD是等边三角形,∴∠ODC=60°,∵MN∥DC,
∴∠FNM=∠ODC=60°,在矩形EFMN中,∠FMN=90°.∴∠NFM=90°﹣∠FNM=30°,
∵NO=3,∴FN=2NO=6,FM=3![]() ,MN=3,∵点F,M分别为OB,OC的中点,
,MN=3,∵点F,M分别为OB,OC的中点,
∴BC=2FM=6![]() ,∴矩形的面积为BCCD=36
,∴矩形的面积为BCCD=36![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个点中,在正比例函数y=﹣5x的图象上的点是( )
A. (1,5)B. (0,5)C. (﹣1,5)D. (5,﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,图形G的投影矩形定义如下:矩形的两组对边分别平行于x轴,y轴,图形G的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的较长的边与较短的边的比为k,我们称常数k为图形G的投影比.如图1,矩形ABCD为△DEF的投影矩形,其投影比
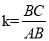 .
.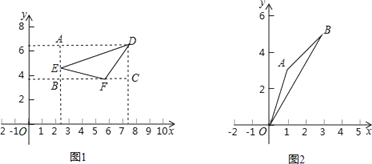
(1)如图2,若点A(1,3),B(3,5),则△OAB投影比k的值为 .
(2)已知点C(4,0),在函数y=2x﹣4(其中x<2)的图象上有一点D,若△OCD的投影比k=2,求点D的坐标.
(3)已知点E(3,2),在直线y=x+1上有一点F(5,a)和一动点P,若△PEF的投影比1<k<2,则点P的横坐标m的取值范围 (直接写出答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=-x+1的图象不经过( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】设x1、x2是一元二次方程2x2﹣4x﹣1=0的两实数根,则x12+x22的值是( )
A. 2 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:S甲2=2,S乙2=1.5,则射击成绩较稳定的是 (填“甲”或“乙“).
相关试题

