【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?

参考答案:
【答案】(1)![]() ;(2)当销售单价x定为每件80元时,厂家每月获得的利润
;(2)当销售单价x定为每件80元时,厂家每月获得的利润![]() 最大,最大利润是4800元.
最大,最大利润是4800元.
【解析】
![]() 根据函数图象经过点
根据函数图象经过点![]() 和点
和点![]() ,利用待定系数法即可求出y与x的函数关系式;
,利用待定系数法即可求出y与x的函数关系式;
![]() 先根据利润
先根据利润![]() 销售数量
销售数量![]() 销售单价
销售单价![]() 成本
成本![]() ,由试销期间销售单价不低于成本单价,也不高于每千克80元,结合电子产品的成本价即可得出x的取值范围,根据二次函数的增减性可得最值.
,由试销期间销售单价不低于成本单价,也不高于每千克80元,结合电子产品的成本价即可得出x的取值范围,根据二次函数的增减性可得最值.
解:![]() 设y与x的函数关系式为
设y与x的函数关系式为![]() ,
,
![]() 函数图象经过点
函数图象经过点![]() 和点
和点![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 与x的函数关系式为
与x的函数关系式为![]() .
.
![]() 由题意得:
由题意得:![]() .
.
![]() 试销期间销售单价不低于成本单价,也不高于每千克80元,且电子产品的成本为每千克40元,
试销期间销售单价不低于成本单价,也不高于每千克80元,且电子产品的成本为每千克40元,
![]() 自变量x的取值范围是
自变量x的取值范围是![]() .
.
![]() ,
,
![]() 当
当![]() 时,w随x的增大而增大,
时,w随x的增大而增大,
![]() 时,w有最大值,
时,w有最大值,
当![]() 时,
时,![]() ,
,
答:当销售单价x定为每件80元时,厂家每月获得的利润![]() 最大,最大利润是4800元.
最大,最大利润是4800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣
 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解该校九年级学生对观看“中国诗词大会”节目喜爱程度,对该校九年级学生进行了随机抽样调查,
 调查时,将喜爱程度分为四级:A级
调查时,将喜爱程度分为四级:A级 非常喜欢
非常喜欢 ,B级
,B级 喜欢
喜欢 ,C级
,C级 一般
一般 ,D级
,D级 不喜欢
不喜欢 根据调查结果,绘制成如下两幅不完整的统计图
根据调查结果,绘制成如下两幅不完整的统计图 请你结合图中信息解答下列问题:
请你结合图中信息解答下列问题: 本次调查共抽取______名学生,在扇形图中,表示A级的扇形的圆心角为______
本次调查共抽取______名学生,在扇形图中,表示A级的扇形的圆心角为______ ;
; 若该校九年级共有学生300人,请你估计不喜欢观看“中国诗词大会”节目的有多少人?并补全条形图;
若该校九年级共有学生300人,请你估计不喜欢观看“中国诗词大会”节目的有多少人?并补全条形图; 已知在A级学生中有3名男生,现要从本次调查中的5名A级学生中,选出2名参加全市中学生诗词大会比赛,请用“列表”或“树形图”的方法,求选出的2名学生中至少有1名女生的概率.
已知在A级学生中有3名男生,现要从本次调查中的5名A级学生中,选出2名参加全市中学生诗词大会比赛,请用“列表”或“树形图”的方法,求选出的2名学生中至少有1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P,BE=BC,PB与CE交于点H,PG∥AD交BC于F,交AB于G,连接CP.下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF.其中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒.

(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境
小明和小丽共同探究一道数学题:
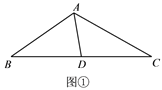
如图①,在△ABC中,点D是边BC的中点,∠BAD=65°,∠DAC=50°,AD=2,
求AC.
探索发现
小明的思路是:延长AD至点E,使DE=AD,构造全等三角形.
小丽的思路是:过点C作CE∥AB,交AD的延长线于点E,构造全等三角形.
选择小明、小丽其中一人的方法解决问题情境中的问题.
类比应用
如图②,在四边形ABCD中,对角线AC、BD相交于点O,点O是BD的中点,

AB⊥AC.若∠CAD=45°,∠ADC=67.5°,AO=2,则BC的长为___________.
相关试题

