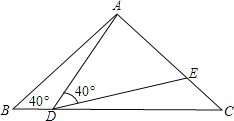
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.

(1)当∠BDA=115°时,∠BAD= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
参考答案:
【答案】(1)25°;小.(2)当DC等于2时,△ABD≌△DCE;(3)当∠ADB=110°或80°时,△ADE是等腰三角形.
【解析】
试题分析:(1)根据三角形内角和定理,将已知数值代入即可求出∠BAD,根据点D的运动方向可判定∠BDA的变化情况.
(2)假设△ABD≌△DCE,利用全等三角形的对应边相等得出AB=DC=2,即可求得答案.
(3)假设△ADE是等腰三角形,分为三种情况:①当AD=AE时,∠ADE=∠AED=40°,根据∠AED>∠C,得出此时不符合;②当DA=DE时,求出∠DAE=∠DEA=70°,求出∠BAC,根据三角形的内角和定理求出∠BAD,根据三角形的内角和定理求出∠BDA即可;③当EA=ED时,求出∠DAC,求出∠BAD,根据三角形的内角和定理求出∠ADB.
解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2)当△ABD≌△DCE时.
DC=AB,
∵AB=2,
∴DC=2,
∴当DC等于2时,△ABD≌△DCE;
(3)∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=![]() (180°﹣40°)=70°,
(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇风力资源丰富,为了实现低碳环保,该乡镇决定开展风力发电,打算购买10台风力发电机组.现有A,B两种型号机组,其中A型机组价格为12万元/台,月均发电量为2.4万kw.h;B型机组价格为10万元/台,月均发电量为2万kw.h.经预算该乡镇用于购买风力发电机组的资金不高于105万元.
(1)请你为该乡镇设计几种购买方案;
(2)如果该乡镇用电量不低于20.4万kw.h/月,为了节省资金,应选择那种购买方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,在等腰
,在等腰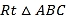 中,
中, ,点E在AC上
,点E在AC上 且不与点A、C重合
且不与点A、C重合 ,在
,在 的外部作等腰
的外部作等腰 ,使
,使 ,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF. 请直接写出线段AF,AE的数量关系;
请直接写出线段AF,AE的数量关系; 将
将 绕点C逆时针旋转,当点E在线段BC上时,如图
绕点C逆时针旋转,当点E在线段BC上时,如图 ,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
,连接AE,请判断线段AF,AE的数量关系,并证明你的结论; 若
若 ,
, ,在图
,在图 的基础上将
的基础上将 绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.


-
科目: 来源: 题型:
查看答案和解析>>【题目】课本“目标与评定”中有这样一道思考题:如图钢架中∠A=20°,焊上等边的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架,若P1A=P1P2,问这样的钢条至多需要多少根?
(1)请将下列解答过程补充完整:
答案:∵∠A=20°,P1A=P1P2,∴∠P1P2A= .
又P1P2=P2P3=P3P4=P4P5,∴∠P2P1P3=P2P3P1=40°,
同理可得,∠P3P2P4=P3P4P2=60°,∠P4P3P5=P4P5P3= ,
∴∠BP4P5=∠CP5P4=100°>90°,
∴对于射线P4B上任意一点P6(点P4除外),P4P5<P5P6,
∴这样的钢架至多需要 根.
(2)继续探究:当∠A=15°时,这样的钢条至多需要多少根?
(3)当这样的钢条至多需要8根时,探究∠A的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣
 与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.
与x轴交于A(1,0),B(﹣3,0)两点,现有经过点A的直线l:y=kx+b1与y轴交于点C,与抛物线的另个交点为D.(1)求抛物线的函数表达式;
(2)若点D在第二象限且满足CD=5AC,求此时直线1的解析式;在此条件下,点E为直线1下方抛物线上的一点,求△ACE面积的最大值,并求出此时点E的坐标;
(3)如图,设P在抛物线的对称轴上,且在第二象限,到x轴的距离为4,点Q在抛物线上,若以点A,D,P,Q为顶点的四边形能否成为平行四边形?若能,请直接写出点Q的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了解该校九年级学生对观看“中国诗词大会”节目喜爱程度,对该校九年级学生进行了随机抽样调查,
 调查时,将喜爱程度分为四级:A级
调查时,将喜爱程度分为四级:A级 非常喜欢
非常喜欢 ,B级
,B级 喜欢
喜欢 ,C级
,C级 一般
一般 ,D级
,D级 不喜欢
不喜欢 根据调查结果,绘制成如下两幅不完整的统计图
根据调查结果,绘制成如下两幅不完整的统计图 请你结合图中信息解答下列问题:
请你结合图中信息解答下列问题: 本次调查共抽取______名学生,在扇形图中,表示A级的扇形的圆心角为______
本次调查共抽取______名学生,在扇形图中,表示A级的扇形的圆心角为______ ;
;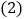 若该校九年级共有学生300人,请你估计不喜欢观看“中国诗词大会”节目的有多少人?并补全条形图;
若该校九年级共有学生300人,请你估计不喜欢观看“中国诗词大会”节目的有多少人?并补全条形图; 已知在A级学生中有3名男生,现要从本次调查中的5名A级学生中,选出2名参加全市中学生诗词大会比赛,请用“列表”或“树形图”的方法,求选出的2名学生中至少有1名女生的概率.
已知在A级学生中有3名男生,现要从本次调查中的5名A级学生中,选出2名参加全市中学生诗词大会比赛,请用“列表”或“树形图”的方法,求选出的2名学生中至少有1名女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量
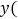 万件
万件 与销售单价
与销售单价 元
元 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示. 求y与x的函数关系式;
求y与x的函数关系式; 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润 最大?最大利润是多少?
最大?最大利润是多少?
相关试题

