【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.

(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)12(2)详见解析(3)详见解析
【解析】
试题分析:①根据等腰三角形性质和勾股定理解答即可;
②根据直角三角形面积求出PD×DC×![]() =15即可求出t;
=15即可求出t;
③根据题意列出PD、MD的表达式解方程组,由于M在D点左右两侧情况不同,所以进行分段讨论即可,注意约束条件.
试题解析:(1)∵AB=AC=13,AD⊥BC,
∴BD=CD=5cm,且∠ADB=90°,
∴AD2=AC2﹣CD2
∴AD=12cm.
(2)AP=t,PD=12﹣t,
又∵由△PDM面积为![]() PD×DC=15,
PD×DC=15,
解得PD=6,∴t=6.
(3)假设存在t,
使得S△PMD=![]() S△ABC.
S△ABC.
①若点M在线段CD上,
即![]() 时,PD=12﹣t,DM=5﹣2t,
时,PD=12﹣t,DM=5﹣2t,
由S△PMD=![]() S△ABC,
S△ABC,
即![]() ,
,
2t2﹣29t+50=0
解得t1=12.5(舍去),t2=2.(2分)
②若点M在射线DB上,即![]() .
.
由S△PMD=![]() S△ABC
S△ABC
得![]() ,
,
2t2﹣29t+70=0
解得![]() ,
,![]() .(2分)
.(2分)
综上,存在t的值为2或![]() 或
或![]() ,使得S△PMD=
,使得S△PMD=![]()
![]() S△ABC.
S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,1),B(2,0),C(4,3).
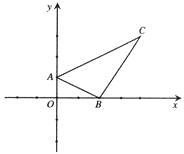
(1)求ΔABC的面积;
(2)设点P在坐标轴上,且ΔABP与ΔABC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列现象不属于投影的是( )
A.皮影B.素描画C.手影D.树影
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:2(a2b+ab2)﹣2(a2b﹣a)﹣2ab2﹣2b的值,其中a、b满足(a+2)2+|b﹣3|=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数y=﹣2(x﹣m)2的图象,下列说法不正确的是( )
A.开口向下
B.对称轴是x=m
C.最大值为0
D.与y轴不相交 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
(1)判断CD与AB的位置关系;
(2)BE与DF平行吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=1时,代数式ax3+bx的值为﹣1,则当x=﹣1时,代数式ax3+bx﹣2的值为( )
A. ﹣4 B. ﹣3 C. ﹣2 D. ﹣1
相关试题

