搜索
【题目】如图，直线l1∥l2∥l3 ， 且l1与l2的距离为1，l2与l3的距离为3．把一块含有45°角的直角三角板如图放置，顶点A、B、C恰好分别落在三条直线上，则△ABC的面积为 ．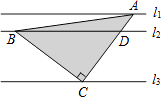 
参考答案：
【答案】
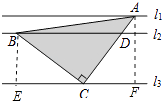
【解析】解：作BE⊥l3于D，作AF⊥3于F，如图所示： 则∠BEC=∠CFA=90°，BE=3，AF=3+1=4，
∴∠ECB+∠EBC=90°，
∵△ABC是等腰直角三角形，
∴∠ACB=90°，AC=BC，
∴∠ECB+∠FCA=90°，
∴∠EBC=∠FCA，
在△BEC和△CFA中，
，
∴△BEC≌△CFA（AAS），
∴CE=AF=4，
∴BC= 
=5，
∴AC=BC=5，
∴S△ABC= 
ACBC= ×5×5= ．
所以答案是 
-
科目： 来源： 题型：
查看答案和解析>>【题目】东坡商贸公司购进某种水果的成本为20元/kg，经过市场调研发现，这种水果在未来48天的销售单价p（元/kg）与时间t（天）之间的函数关系式为：
，且其日销售量y（kg）与时间t（天）的关系如下表：
（1）已知y与t之间的变化规律符合一次函数关系，试求在第30天的日销售量是多少？
（2）问哪一天的销售利润最大？最大日销售利润为多少？
（3）在实际销售的前24天中，公司决定每销售1kg水果就捐赠n元利润（n＜9）给“精准扶贫”对象．现发现：在前24天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求n的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）0﹣3﹣（﹣4）+2
（2）﹣22+3×（﹣1）4﹣（﹣4）×5
（3）（
﹣ 
+ 
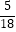）×（﹣18）
（4）（﹣5）×（﹣3
）+（﹣7）×（﹣3 ）+2×（﹣3 ） -
科目： 来源： 题型：
查看答案和解析>>【题目】某垃圾分类试点小区对3 月份该小区产生的四类垃圾（可回收物、厨余垃圾、有害垃圾、其他垃圾）的重量（单位：吨）进行统计，下图是还未制作完整的统计图.
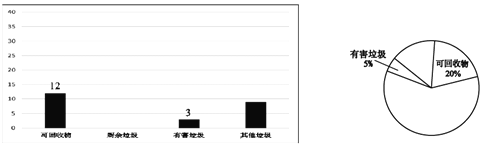
（1）根据图中信息，该小区3月份共产生多少吨垃圾？
（2）垃圾分类投放后，每吨厨余垃圾可生产0.3吨有机肥料.若该小区3月份的厨余垃圾共生产10.8 吨有机肥料，请将图9中的信息补充完整.
-
科目： 来源： 题型：
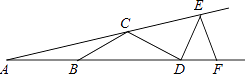
查看答案和解析>>【题目】如图，△EAF=15°，AB=BC=CD=DE=EF，则∠DEF等于（ ）
A.90°
B.75°
C.70°
D.60° -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC在平面直角坐标系中，点A、B、C的坐标分别为A（﹣2，1），B（﹣4，5），C（﹣5，2）．
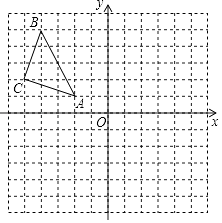
（1）画出△ABC关于y对称的△A1B1C1 ， 其中，点A、B、C的对应点分别为A1、B1、C1；
（2）直接写出点A1、B1、C1的坐标； A1 ， B1 ， C1 ．
（3）△A1B1C1的面积是 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】小松调查了七年级（1）班50名同学最喜欢的篮球明星，结果如下：
B B C A A B C D C B C A D D B A C C B A
A B D A C C A B A C A B C D A C C A C A
A A A C A D B C C A
其中A代表科比，B代表库里，C代表詹姆斯，D代表格里芬，用扇形统计图表示该班同学最喜欢的篮球明星的情况，则表示喜欢科比的扇形的圆心角是（用度分秒表示）．
相关试题
