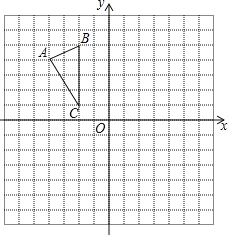
【题目】如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣4,4),B(﹣2,5),C(﹣2,1).
(1)平移△ABC,使点C移到点C1(﹣2,﹣4),画出平移后的△A1B1C1,并写出点A1,B1的坐标;
(2)将△ABC绕点(0,3)旋转180°,得到△A2B2C2,画出旋转后的△A2B2C2;
(3)求(2)中的点C旋转到点C2时,点C经过的路径长(结果保留π).
参考答案:
【答案】(1)画图见解析, A1(﹣4,﹣1),B1(﹣2,0);(2)画图见解析;(3)点C经过的路径长为2![]() π.
π.
【解析】(1)根据点C移到点C1(-2,-4),可知向下平移了5个单位,分别作出A、B、C的对应点A1、B1、C1即可解决问题;
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2即可;
(3)利用勾股定理计算CC2,可得半径为2![]() ,根据圆的周长公式计算即可.
,根据圆的周长公式计算即可.
(1)如图所示,则△A1B1C1为所求作的三角形,
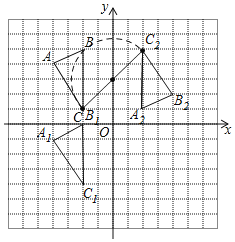
∴A1(-4,-1),B1(-2,0);
(2)如图所示,则△A2B2C2为所求作的三角形,
(3)点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,
由勾股定理得:CC2=![]() ,
,
∴点C经过的路径长:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足
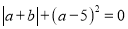 .
.(1)点A的坐标为 ;点B的坐标为 ;
(2)如图1,若点C的坐标为(-3,-2),且BE⊥AC于点E,OD⊥OC交BE延长线于D,试求点D的坐标;
(3)如图2,M、N分别为OA、OB边上的点,OM=ON,OP⊥AN交AB于点P,过点P 作PG⊥BM,交AN的延长线于点G,请写出线段AG、OP与PG之间的数量关系,并证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
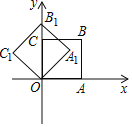
A. (1,1) B. (0,
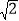 ) C. (
) C. ( ) D. (﹣1,1)
) D. (﹣1,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】为了完成“舌尖上的中国”的录制,节目组随机抽查了某省“A.奶制品类,B.肉制品类,C.面制品类,D.豆制品类”四类特色美食若干种,将收集的数据整理并绘制成下面两幅尚不完整的统计图,请根据图中信息完成下列问题:
(1)这次抽查了四类特色美食共 种,扇形统计图中a= ,扇形统计图中A部分圆心角的度数为 ;
(2)补全条形统计图;
(3)如果全省共有这四类特色美食120种,请你估计约有多少种属于“豆制品类”?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在运动会前夕,育红中学都会购买篮球、足球作为奖品.若购买10个篮球和15个足球共花费3000元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元?
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1050元,则最多可购买多少个篮球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;
(2)点M,N分别在直线AD,AC上,且∠BMN=90°.
①如图2,当点M在AD的延长线上时,求证:AB+AN=
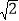 AM;
AM;②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长.

相关试题

