【题目】 如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
(1)求证:PD是⊙O的切线;
(2)如图2,点M是 ![]() 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A= ![]() ,求
,求 ![]() 的值.
的值.
参考答案:
【答案】
(1)解:连结OD;

∵AB是⊙O的直径,
∴∠ADB=90°,OA=OB,∠A+∠ABD=90°;
又∵OA=OB=OD,
∴∠ADO=∠A,∠BDO=∠ABD;
又∵∠A=∠PDB,
∴∠PDB+∠BD0=90°,
即∠PDO=90°,且D在圆上,
∴PD是⊙O的切线;
(2)解:连结OM,过D作DF⊥AB于F;
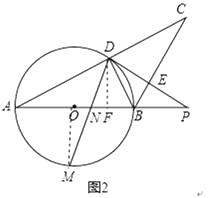
∵点M是 ![]() 的中点,
的中点,
∴OM⊥AB;设BD=x,
∵tan∠A= ![]() =
= ![]() ,
,
∴AD=4x;由勾股定理得:
AB= ![]() =
= ![]() x;由三角形的面积公式得:
x;由三角形的面积公式得: ![]() ADBD=
ADBD= ![]() ABDF,
ABDF,
∴DF= ![]() x,
x,
∵OM∥DF,
∴△OMN∽△FDN,
∴ ![]() =
= ![]() =
= ![]() .
.
【解析】(1)连结OD;由AB是⊙O的直径,得到ADB=90°,根据等腰三角形的性质得到∠ADO=∠A,∠BDO=∠ABD;得到∠PDO=90°,且D在圆上,于是得到结论;(2)连结OM,过D作DF⊥AB于F;由点M是 ![]() 的中点,得到OM⊥AB;设BD=x,根据已知条件得到AD=4x;由勾股定理得到AB=
的中点,得到OM⊥AB;设BD=x,根据已知条件得到AD=4x;由勾股定理得到AB= ![]() =
= ![]() x;根据三角形的面积公式解方程得到DF=
x;根据三角形的面积公式解方程得到DF= ![]() x,根据相似三角形的性质即可得到结论.
x,根据相似三角形的性质即可得到结论.
【考点精析】本题主要考查了相似三角形的判定与性质和解直角三角形的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步落实《中华人民共和国民办教育促进法》,某市教育局拿出了b元资金建立民办教育发展基金会,其中一部分作为奖金发给了n所民办学校.奖金分配方案如下:首先将n所民办学校按去年完成教育、教学工作业绩(假设工作业绩均不相同)从高到低,由1到n排序,第1所民办学校得奖金
 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.(1)请用n、b分别表示第2所、第3所民办学校得到的奖金;
(2)设第k所民办学校所得到的奖金为
 元(1
元(1 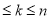 ),试用k、n和b表示
),试用k、n和b表示 (不必证明);
(不必证明);(3)比较
 和
和 的大小(k=1,2 ,……,
的大小(k=1,2 ,……,  ),并解释此结果关于奖金分配原则的实际意义.
),并解释此结果关于奖金分配原则的实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1 100元,请问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并指出获利最大的购货方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )

A.24 B.12 C.6 D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2+a3=a5B.a2·a3=a6C.(a2)3=a6D.a6÷a2=a3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果某三角形的两边长分别为5和7,第三边的长为偶数,那么这个三角形的周长可以是( )
A.13B.14C.15D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AC交BD于点O,点E、点F分别是OA、OC的中点,请判断线段BE、DF的关系,并证明你的结论

相关试题

