【题目】如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE. 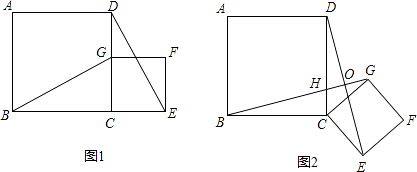
(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系,不必证明;
(2)将图1中的正方形CEFG绕着点C按顺时针方向旋转任意角度α,得到如图2情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立,并证明你的判断.
参考答案:
【答案】
(1)解:延长BG交DE于点H,
在△BCG与△DCE中,
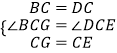 ,
,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠EDC,BG=DE,
∵∠BGC=∠DGH,
∴∠DHB=∠BCG=90°,
∴BG⊥DE
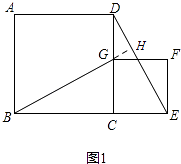
(2)解:BG=DE,BG⊥DE仍然成立
如图2,∠BCD+∠DCG=∠ECG+∠DCG,
即∠BCG=∠DCE,
在△BCG与△DCE中,
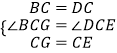 ,
,
∴△BCG≌△DCE(SAS),
∴∠GBC=∠EDC,BG=DE,
∵∠BHC=∠DHG,
∴∠BCD=∠DOB=90°,
即BG⊥DE
【解析】(1)延长BG交DE于点H,易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠DHB=90°;(2)易证△BCG≌△DCE,所以∠GBC=∠EDC,BG=DE,所以∠BCD=90°.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某班学生每天使用零花钱的情况,张华随机调查了30名同学,结果如下表:
每天使用零花钱(单位:元)
1
2
3
4
5
人数
2
5
8
9
6
则这30名同学每天使用的零花钱的众数和中位数分别是( )
A.4,3
B.4,3.5
C.3.5,3.5
D.3.5,4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H, 连接OH,求证:∠DHO=∠DCO.
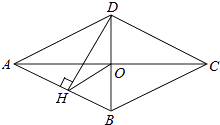
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:60,30,40,50,70,这组数据的平均数和中位数分别是( )
A. 60,50 B. 50,60 C. 50,50 D. 60,60
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,若点M在抛物线y=(x﹣3)2﹣4的对称轴上,则点M的坐标可能是( )
A.(1,0)B.(3,5)C.(﹣3,﹣4)D.(0,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上有三个点A、B、C(如图).请回答:
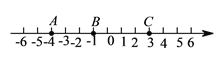
(1)写出数轴上与点B相距5个单位的点M所表示的数为 ;
(2)在数轴上表示:将点C向左移动6个单位到达点D,点A的相反数为点E,并用“<”号把B、D、E三点所表示的数连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形OABC的顶点B在第一象限,点C在x轴上,点A在y轴上,D、E分别是AB,OA中点.过点D的双曲线
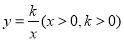 与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).
与BC交于点G.连接DC,F在DC上,且DF:FC=3:1,连接DE,EF.若△DEF的面积为6,则k的值为( ).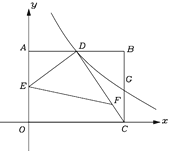
A.
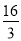 B.
B. 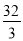 C. 6 D. 10
C. 6 D. 10
相关试题

