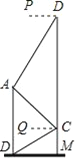
【题目】如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据: ![]() ≈1.73).
≈1.73).
参考答案:
【答案】雕塑AB的高约是6.3m.
【解析】试题分析:过A作AR⊥DM,垂足是R,在Rt△ARD中利用三角函数求得AR的长,延长CQ交AB于点N,在Rt△ANC中利用三角函数求得AN的长,在Rt△CNB中求得NB的长,根据AB=BN+AN求解.
试题解析:过A作AR⊥DM,垂足是R.
∵∠PDA=60°,∴∠ADR=30°,
在Rt△ARD中,AR=ADsin30°=8×![]() =4(m),
=4(m),
延长CQ交AB于点N.
在Rt△ANC中,∠ANC=90°,∠ACN=45°,∴AN=NC=AR=4(m),
在Rt△CNB中,∠CNB=90°,∠NCB=30°,∴NB=CNtan30°=4×![]() =
=![]() (m).
(m).
∴AB=BN+AN=![]() +4≈6.3(m).
+4≈6.3(m).
答:雕塑AB的高约是6.3m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)8m4.(-12m3n5)÷(-2mn)4; (2)(3x+2y)(2x-3y)-3x(3x-2y).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(am+1bn+2)(a2mb2n﹣1)=a4b7 , 则m+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x2+kx+25是一个完全平方式,则k= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD.
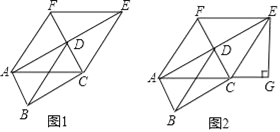
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG=
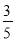 ,则AD= (直接填空)
,则AD= (直接填空) -
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A. 4cmB. 2cm;C. 小于2cmD. 不大于2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“两直线平行、同旁内角互补”中,题设是_________,结论是_______,此命题是_______命题.
相关试题

