【题目】某学校计划购买一批课外读物,为了了解学生对课外读物的需求情况,学校进行了一次“我最喜爱的课外读物”的调查,设置了“文学”、“科普”、“艺术”和“其他”四个类别,规定每人必须并且只能选择其中一类,现从全体学生的调查表中随机抽取了部分学生的调查表进行统计,并把统计结果绘制了如图所示的两幅不完整的统计图.
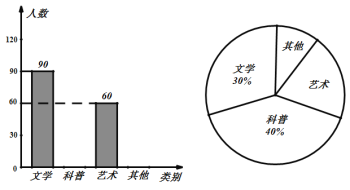
(1) 从全体学生的调查表中随机抽取了多少名学生?
(2) 将条形图补充完整;
(3) 艺术类读物所在扇形的圆心角是多少度?
参考答案:
【答案】(1)300;(2)见详解;(3)72°.
【解析】
(1)由文学类人数及其所占百分比可得总人数;
(2)总人数乘以科普类所占百分比可得其人数,用总人数减去另外三个类别人数求得“其他”的人数即可补全图形;
(3)用360°乘以艺术类人数所占比例可得.
解:(1)抽取调查的总人数为:90÷30%=300(人),
∴从全体学生的调查表中随机抽取了300名学生;
(2)科普类数量为300×40%=120,其他类别的数量为300-(90+60+120)=30,
补全图形如下:
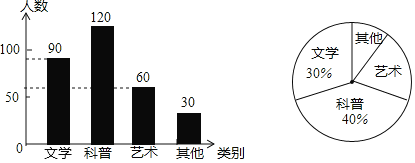
(3)艺术类读物所在扇形的圆心角是360°×![]() =72°,
=72°,
∴艺术类读物所在扇形的圆心角是72°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
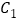 :
: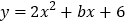 与抛物线
与抛物线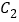 关于y轴对称, 抛物线
关于y轴对称, 抛物线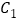 与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.
与x轴分别交于点A(-3, 0), B(m, 0), 顶点为M.(1)求b和m的值;
(2)求抛物线
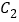 的解析式;
的解析式;(3)在x轴, y轴上分别有点P(t, 0), Q(0, -2t), 其中t>0, 当线段PQ与抛物线
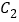 有且只有一个公共点时,求t的取值范围.
有且只有一个公共点时,求t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
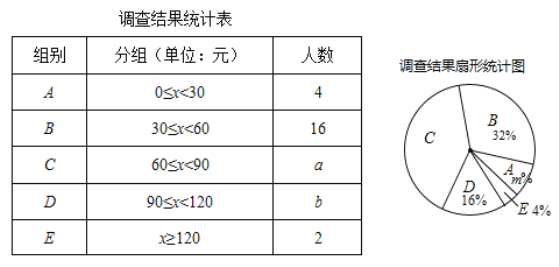
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__________人,a+b=__________,m=__________;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额在60≤x<120范围的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证
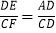 ;
;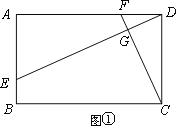


(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得
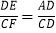 成立?并证明你的结论;
成立?并证明你的结论;(3)如图③,若BA=BC=4,DA=DC=6,∠BAD=90°,DE⊥CF,请直接写出
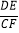 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=
 ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )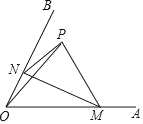
A.
 B.
B.  C. 6 D. 3
C. 6 D. 3 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,已知
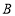 、
、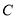 两点把线段
两点把线段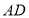 分成
分成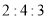 三部分,
三部分,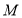 是
是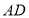 的中点,若
的中点,若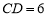 ,求线段
,求线段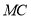 的长.
的长. 
(2)如图
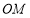 、
、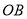 、
、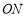 是
是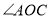 内的三条射线,
内的三条射线,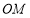 、
、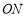 分别是
分别是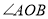 、
、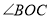 的平分线,
的平分线,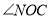 是
是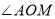 的3倍,
的3倍,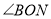 比
比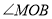 大
大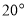 ,求
,求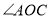 的度数.
的度数. 
相关试题

