【题目】如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;(2)AB与CD平行吗?请说明理由.

参考答案:
【答案】(1)△ABF与△DCE全等,理由见解析;(2)AB与CD平行,理由见解析.
【解析】
(1)先根据平行线的性质∠AFB=∠DEC,然后利用“ASA”可判断△ABF≌△DCE;
(2)根据△ABF≌△DCE,则∠A=∠D,再利用平行线的判定定理可得结论.
证明:(1)△ABF与△DCE全等,
理由是:∵CE∥BF,∴∠AFB=∠DEC,
在△ABF和△DCE中,
 ,
,
∴△ABF≌△DCE(ASA);
(2)AB与CD平行,
理由是:∵△ABF≌△DCE,
∴∠A=∠D(全等三角形的对应角相等),
∴AB∥CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
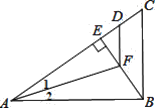
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )

A. △AOB≌△DOC B. △ABO≌△DOC C. ∠A=∠C D. ∠B=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为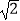 .
.
其中正确结论的个数是( )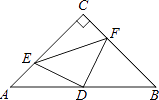
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 .
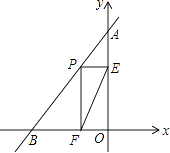
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有多少千米?
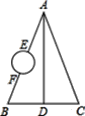
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;
(3)在图3中,画一个正方形,使它的面积是10.
相关试题

