【题目】如图,直线AB的解析式为y=2x+5,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为 . 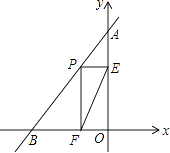
参考答案:
【答案】![]()
【解析】解:∵一次函数y=2x+5中,令x=0,则y=5,令y=0,则x=﹣ ![]() ,
,
∴A(0,5),B(﹣ ![]() ,0).
,0).
∵PE⊥y轴于点E,PF⊥x轴于点F,
∴四边形PEOF是矩形,且EF=OP,
∵O为定点,P在线段上AB运动,
∴当OP⊥AB时,OP取得最小值,此时EF最小,
∵A(0,5),点B坐标为(﹣ ![]() ,0),
,0),
∴OA=5,O B= ![]() ,
,
由勾股定理得:AB= ![]() =
= ![]() =
= ![]() ,
,
∴ABOP=OAOB,
∴OP= ![]() =
= ![]() =
= ![]() .
.
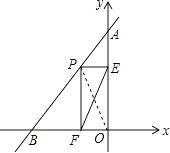
所以答案是: ![]() .
.
【考点精析】通过灵活运用一次函数的性质,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD,BC相交于点O,OA=OD,OB=OC.下列结论正确的是( )

A. △AOB≌△DOC B. △ABO≌△DOC C. ∠A=∠C D. ∠B=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为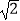 .
.
其中正确结论的个数是( )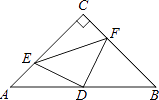
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、E、F、D四点在同一直线上,CE∥BF,CE=BF,∠B=∠C.(1)△ABF与△DCE全等吗?请说明理由;(2)AB与CD平行吗?请说明理由.

-
科目: 来源: 题型:
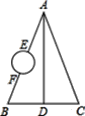
查看答案和解析>>【题目】如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个直角三角形,使它们的三边长都是无理数;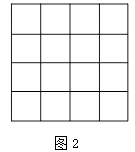
(3)在图3中,画一个正方形,使它的面积是10.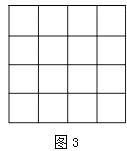
-
科目: 来源: 题型:
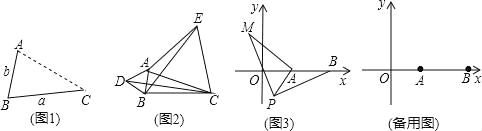
查看答案和解析>>【题目】(1)发现:
如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:
点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:
如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.
相关试题

