搜索
【题目】某治安巡警分队常常在一条东西走向的街道上巡逻一天 下午，该巡警分队驾驶电动小汽车从位于这条街道上的某岗亭出发巡逻，如果规定向东为正，向西为负，他们行驶里程(单位： km)如下：
问：
(1)这辆小汽车完成巡逻后位于该岗亭的那一侧？距离岗亭有多少千米？
(2)已知这种电动小汽车平均每千米耗电
度，则这天下午小汽车共耗电多少度？
参考答案：
【答案】（1）这辆小汽车完成上述巡逻后在岗亭的东侧，距离岗亭有
千米；（2）这天下午小汽车共耗电
度．
【解析】
（1）将行驶里程数相加，和为正则在东侧，和为负则在西侧；
（2）将行驶里程数据的绝对值相加则为总路程，再乘以
即可．
解：
答：这辆小汽车完成上述巡逻后在岗亭的东侧，距离岗亭有千米．
(度)
答：这天下午小汽车共耗电度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的一块地，∠ADC＝90°，AD＝12m，CD＝9m，AB＝39m，BC＝36m，求这块地的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】兴隆商场用36万元购进A、B两种品牌的服装，销售完后共获利6万元，其进价和售价如下表：
该商场购进A、B两种服装各多少件？
（2）第二次以原价购进A、B两种服装，购进B服装的件数不变，购进A服装的件数是第一次的2倍，A种服装按原价出售，而B种服装打折销售；若两种服装销售完毕，要使第二次销售活动获利不少于81600元，则B种服装最低打几折销售？
-
科目： 来源： 题型：
查看答案和解析>>【题目】对x，y定义一种新运算T，规定：T（x，y）＝
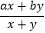（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）＝
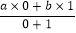＝b，已知T（1，1）＝2.5，T（4，﹣2）＝4．（1）求a，b的值；
（2）若关于m的不等式组
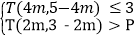恰好有2个整数解，求实数P的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．
（1）求新传送带AC的长度；
（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．（说明：（1）（2）的计算结果精确到0.1米，参考数据：
≈1.41， 
≈1.73， 
≈2.24， 
≈2.45） -
科目： 来源： 题型：
查看答案和解析>>【题目】“端午节”所示我国的传统佳节，民间历来有吃“粽子”的习俗，我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽（以下分别用A、B、C、D表示）这四种不用口味粽子的喜爱情况，在节前对某居民区进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）．
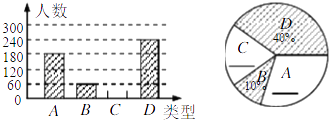
请根据以上信息回答：
（1）本次参加抽样调查的居民有多少人？
（2）将两幅不完整的图补充完整；
（3）若居民区有8000人，请估计爱吃D粽的人数；
（4）若有外型完全相同的A、B、C、D粽各一个，煮熟后，小王吃了两个，用列表或画树状图的方法，求他第二个恰好吃到的是C粽的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．
（1）弦AB=（结果保留根号）；
（2）当∠D=20°时，求∠BOD的度数．
相关试题
