【题目】(8分)已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2=![]() x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.
参考答案:
【答案】x>2或x<﹣2
【解析】试题分析:(1)根据OC的长度确定出n的值为8或-8,然后分①n=8时求出点A的坐标,然后确定抛物线开口方向向下并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围;②n=-8时求出点A的坐标,然后确定抛物线开口方向向上并求出点B的坐标,再求出抛物线的对称轴解析式,然后根据二次函数的增减性求出x的取值范围.
试题解析:根据OC长为8可得一次函数中的n的值为8或﹣8.
分类讨论:①n=8时,易得A(﹣6,0)如图1,

∵抛物线经过点A、C,且与x轴交点A、B在原点的两侧,
∴抛物线开口向下,则a<0,
∵AB=16,且A(﹣6,0),
∴B(10,0),而A、B关于对称轴对称,
∴对称轴直线x=![]() =2,
=2,
要使y1随着x的增大而减小,则a<0,
∴x>2;
②n=﹣8时,易得A(6,0),如图2,

∵抛物线过A、C两点,且与x轴交点A,B在原点两侧,
∴抛物线开口向上,则a>0,
∵AB=16,且A(6,0),
∴B(﹣10,0),而A、B关于对称轴对称,
∴对称轴直线x=![]() =﹣2,
=﹣2,
要使y1随着x的增大而减小,且a>0,
∴x<﹣2.
综上所述,x>2或x<2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:
(1)3m2n-12mn+12n. (2)(a+b)3-4(a+b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x,y)在第四象限,且|x|=3, |y|=5,则点P的坐标是( )
A. (-3,5)B. (3, -5).C. (5, -3)D. (-5,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)已知关于
 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根 、
、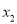 .
.(1)求
 的取值范围;
的取值范围; (2)试说明
 ,
, 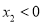 ;
; (3)若抛物线
 与
与 轴交于
轴交于 、
、 两点,点
两点,点 、点
、点 到原点的距离分别为
到原点的距离分别为 、
、 ,且
,且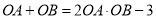 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若( )×(-xy)=3x2y2,则括号里应填的单项式是( )
A. -3y B. 3xy C. -3xy D. 3x2y
-
科目: 来源: 题型:
查看答案和解析>>【题目】在实数范围内规定新运算“△”其规则是:a△b=a+b﹣1,则x△(x﹣2)>3的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+kx+4可以用完全平方公式进行因式分解,则k的值为( )
A. -4 B. 2 C. 4 D. ±4
相关试题

