【题目】若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=50°,则∠BOC=_______度.

参考答案:
【答案】65°
【解析】
利用三角形内角和定理求得∠ABC+∠ACB=130°,根据三角形外角性质得到∠CBE=∠A+∠ACB,∠BCF=∠A+∠ABC,进而求得∠CBE+∠BCF=230°,根据角平分线定义可知
∠1=∠2=![]() ∠CBE,∠3=∠4=
∠CBE,∠3=∠4=![]() ∠BCF,进而求得∠2+∠3=115°,最后利用三角形内角和定理即可解决问题.
∠BCF,进而求得∠2+∠3=115°,最后利用三角形内角和定理即可解决问题.
∵∠A+∠ABC+∠ACB=180°,∠A=50°,
∴∠ABC+∠ACB=130°
∵∠CBE、∠BCF是△ABC的外角
∴∠CBE=∠A+∠ACB,∠BCF=∠A+∠ABC
∴∠CBE+∠BCF=∠A+∠ACB+∠A+∠ABC=230°
∵OB、OC分别平分∠CBE、∠BCF
∴∠1=∠2=![]() ∠CBE,∠3=∠4=
∠CBE,∠3=∠4=![]() ∠BCF
∠BCF
∴∠2+∠3=![]() (∠CBE+∠BCF)=115°
(∠CBE+∠BCF)=115°
∵∠2+∠3+∠BOC=180°
∴∠BOC=65°
故答案为:65°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与x轴、y轴分别交于C、D两点,与双曲线
与x轴、y轴分别交于C、D两点,与双曲线 在第一象限内交于点P,过点P作
在第一象限内交于点P,过点P作 轴于点A,
轴于点A, 轴于点B,已知
轴于点B,已知 且
且
 直接写出直线的解析式______,双曲线的解析式______;
直接写出直线的解析式______,双曲线的解析式______; 设点Q是直线
设点Q是直线 上的一点,且满足
上的一点,且满足 的面积是
的面积是 面积的2倍,请求出点Q的坐标.
面积的2倍,请求出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2﹣
x2﹣ x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在
 中,
中, 于E,
于E, ,D是AE上的一点,且
,D是AE上的一点,且 ,连接BD,CD.
,连接BD,CD.
 试判断BD与AC的位置关系和数量关系,并说明理由;
试判断BD与AC的位置关系和数量关系,并说明理由; 如图2,若将
如图2,若将 绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由; 如图3,若将
如图3,若将 中的等腰直角三角形都换成等边三角形,其他条件不变.
中的等腰直角三角形都换成等边三角形,其他条件不变. 试猜想BD与AC的数量关系,请直接写出结论;
试猜想BD与AC的数量关系,请直接写出结论; 你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次质检抽测中,随机抽取某摊位20袋食盐,测得各袋的质量分别为(单位:g):492,496,494,495,498,497,501,502,504,496,497,503,506,508,507,492,496,500,501,499,根据以上抽测结果,任买一袋该摊位的食盐,质量在497.5 g~501.5 g之间的概率为( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A.
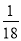 B.
B. 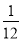 C.
C. 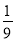 D.
D. 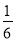
相关试题

