【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

参考答案:
【答案】(1)∠EBC=30°;(2)△ABC的周长= 26.
【解析】
(1)根据等腰三角形的性质和三角形内角和定理求出∠ABC的度数,根据线段的垂直平分线的性质求出∠EBA的度数,计算即可;
(2)根据线段的垂直平分线的性质和三角形的周长公式求出AC+BC+AB=16+5+5=26,计算即可.
(1)∵AB=AC,∠A=40°,∴∠ABC=∠C=70°.
∵DE是AB的垂直平分线,∴EA=EB,∴∠EBA=∠A=40°,∴∠EBC=30°;
(2)∵DE是AB的垂直平分线,∴DA=BD=5,EB=AE,△EBC的周长=EB+BC+EC=EA+BC+EC=AC+BC=16,则△ABC的周长=AB+BC+AC=26.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640
6430
6520
6798
7325
8430
8215
7453
7446
6754
7638
6834
7326
6830
8648
8753
9450
9865
7290
7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表组别
步数分组
频数
A
5500≤x<6500
2
B
6500≤x<7500
10
C
7500≤x<8500
m
D
8500≤x<9500
3
E
9500≤x<10500
n
请根据以上信息解答下列问题:
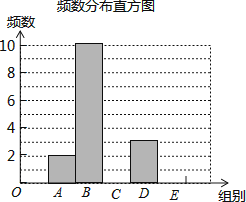
(1)填空:m= , n=
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在边长为1个单位长度的小正方形组成的网络中,给出了格点△ABC(顶点是网络线的交点)和点A1.画出一个格点A1B1C1,使它与△ABC全等且A与A1是对应点;
(2)如图②,已知△ABC 的三个顶点的坐标分别为A(-3,-3),B(-2,-1)C(-1,-2).
①画出△ABC关于x轴对称的图形;
②点B关于y轴对称的点的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
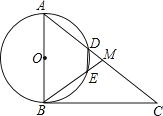
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE=;
②连接OD,OE,当∠A的度数为时,四边形ODME是菱形. -
科目: 来源: 题型:
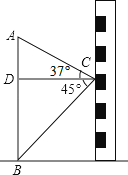
查看答案和解析>>【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
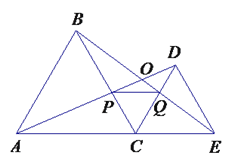
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
相关试题

