【题目】如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)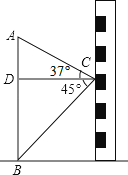
参考答案:
【答案】解:在Rt△BCD中,BD=9米,∠BCD=45°,则BD=CD=9米.
在Rt△ACD中,CD=9米,∠ACD=37°,则AD=CDtan37°≈9×0.75=6.75(米).
所以,AB=AD+BD=15.75米,
整个过程中旗子上升高度是:15.75﹣2.25=13.5(米),
因为耗时45s,
所以上升速度v= ![]() =0.3(米/秒).
=0.3(米/秒).
答:国旗应以0.3米/秒的速度匀速上升
【解析】通过解直角△BCD和直角△ACD分别求得BD、CD以及AD的长度,则易得AB的长度,则根据题意得到整个过程中旗子上升高度,由“速度= ![]() ”进行解答即可.本题考查了解直角三角形的应用﹣仰角俯角问题.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
”进行解答即可.本题考查了解直角三角形的应用﹣仰角俯角问题.解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,在边长为1个单位长度的小正方形组成的网络中,给出了格点△ABC(顶点是网络线的交点)和点A1.画出一个格点A1B1C1,使它与△ABC全等且A与A1是对应点;
(2)如图②,已知△ABC 的三个顶点的坐标分别为A(-3,-3),B(-2,-1)C(-1,-2).
①画出△ABC关于x轴对称的图形;
②点B关于y轴对称的点的坐标为

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
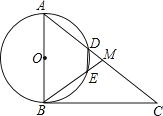
(1)求证:MD=ME;
(2)填空:
①若AB=6,当AD=2DM时,DE=;
②连接OD,OE,当∠A的度数为时,四边形ODME是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°. 恒成立的结论有( )
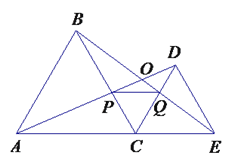
A. ①③④⑤ B. ①②④⑤
C. ①②③⑤ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=4.2cm,则AD=______.

相关试题

