【题目】如图,直线y=2x﹣4的图象与x、y轴交于B、A两点,与y=![]() 的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为 .
的图象交于点C,CD⊥x轴于点D,如果△CDB的面积:△AOB的面积=1:4,则k的值为 .

参考答案:
【答案】6.
【解析】
试题分析:由直线y=2x﹣4的图象与x,y轴交于B,A两点,可求得A与B的坐标,易得△AOB∽△CDB,然后由相似三角形面积比等于相似比的平方,求得CD与BD的长,继而求得点C的坐标,则可求得答案.
解:∵直线y=2x﹣4的图象与x,y轴交于B,A两点,
∴点A(0,﹣4),点B(2,0),
∴OA=4,OB=2,
∵CD⊥x轴,
∴CD∥OA,
∴△AOB∽△CDB,
∵△CDB的面积:△AOB的面积=1:4,
∴![]() =
=![]() ,
,
∴CD=2,BD=1,
∴OD=OB+BD=3,
∴点C的坐标为:(3,2),
∴2=![]() ,
,
解得:k=6.
故答案为:6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣5,y1),(0,y2)都在直线y=﹣3x+2上,则y1 , y2的大小关系是
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2 , 当﹣1≤x≤3时,y的取值范围是( )
A.﹣1≤y≤9
B.0≤y≤9
C.1≤y≤9
D.﹣1≤y≤3 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)(x﹣1)3=27
(2)2x2﹣50=0. -
科目: 来源: 题型:
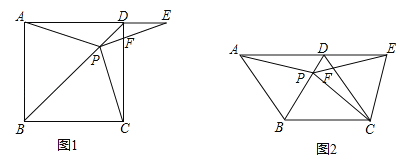
查看答案和解析>>【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.(1)求证:PC=PE; (2)求∠CPE的度数;
拓展探究
(3)如图2,把“正方形ABCD”改为“菱形ABCD”,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形是全等三角形的是( )
A.两个含60°角的直角三角形
B.腰对应相等的两个等腰直角三角形
C.边长为3和4的两个等腰三角形
D.一个钝角相等的两个等腰三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】64的立方根是( )
A. 8 B. 4 C. ﹣8 D. ±8
相关试题

