【题目】在三角形AOB和三角形COD中,∠AOB=∠COD,
(1)已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.
(2)已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.
(3)当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD.

参考答案:
【答案】(1)∠AOC=150°;(2)∠BOD=60°;(3)∠AOC+∠DOB=2α.
【解析】
(1)由图可知∠AOC=∠AOB+∠BOC,∠DOB=∠DOC﹣∠BOC,根据角的和差关系可得结果;
(2)由图可知∠AOC=∠AOB+∠BOC,∠DOB=∠DOC﹣∠BOC,根据角的和差关系可得结果;
(3)由图可知∠AOC=∠AOB+∠BOC,∠DOB=∠DOC﹣∠BOC,根据角的和差关系可得结果.
解:(1)∵∠AOC=∠AOB+∠BOC=90°+∠BOC,
∠DOB=∠DOC﹣∠BOC=90°﹣∠BOC,
∴∠AOC+∠DOB=90°+∠BOC+90°﹣∠BOC=180°,
∵∠BOD=30°,
∴∠AOC=150°;
(2)∵∠AOC=∠AOB+∠BOC=90°+∠BOC,
∠DOB=∠DOC﹣∠BOC=90°﹣∠BOC,
∴∠AOC+∠DOB=90°+∠BOC+90°﹣∠BOC=180°,
∵∠AOC=2∠BOD,
∴∠BOD=60°;
(3)∵∠AOC=∠AOB+∠BOC=α+∠BOC,
∠DOB=∠DOC﹣∠BOC=α﹣∠BOC,
∴∠AOC+∠DOB=α+∠BOC+α﹣∠BOC=2α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来数的情况下,为估计白球数,小刚向其中放入8个黑球摇匀后,从中随意摸出一个球记下颜色,再把它放回盒中,不断重复这一过程,共摸球100次,其中20次摸到黑球,你估计盒中大约有白球( )
A.20个
B.28个
C.36个
D.32个 -
科目: 来源: 题型:
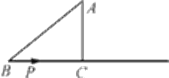
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开设篮球、足球、乒乓球、排球四个项目的选修课,为了解同学们的报名情况,随机抽取了部分学生进行调査,将获得的数据进行整理,绘制了如下两幅不完整的统计图,请你根据统计图提供的信息,完成下列问题:

(1)把条形统计图1补充完整,写出图2中C所在扇形的圆心角是 °;
(2)若该校有3000名学生,请你估计全校大约有多少名学生会选修足球课.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组将边长为3的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )

A.6
B.7
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
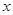 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
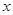 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
相关试题

