【题目】小明同学准备从家打车去南坪,出门后发现到了拥堵使得车辆停滞不前,等了几分钟后他决定步行前往地铁站乘地铁直达南坪站(忽略中途等站和停靠站的时间),在此过程中,他离南坪站的距离y(km)与时间x(h)的函数关系的大致图象是( )
A. 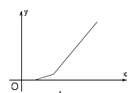 B.
B. 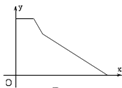
C.  D.
D. 
参考答案:
【答案】D
【解析】
根据小明同学有急事准备从南开中学去南坪,他出校门后发现道路拥堵使得车辆停滞不前,等了几分钟此时他离南坪站的距离没有变化;
然后她步行前往地铁站他离南坪站的距离y(km)随时间x(h)的增大而减小;
最后她乘地铁直达南坪站他离南坪站的距离y(km)随时间x(h)的增大而减小,并且增加的速度更快了,即可得出函数的大致图象.
小明同学出校门后发现道路拥堵使得车辆停滞不前,等了几分钟,他离南坪站的距离没有变化,
然后她步行前往地铁站他离南坪站的距离y(km)随时间x(h)的增大而减小,
最后她乘地铁直达南坪站他离南坪站的距离y(km)随时间x(h)的增大而减小,并且增加的速度更快了,
符合以上的图象是D.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
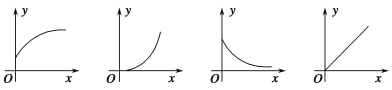
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,过点B做射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,连接DF,设运动的时间为t秒(t>0).
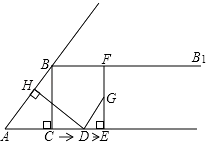
(1)当t为时,AD=AB,此时DE的长度为;
(2)当△DEF与△ACB全等时,求t的值;
(3)以DH所在直线为对称轴,线段AC经轴对称变换后的图形为A′C′.
①当t>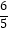 时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
时,设△ADA′的面积为S,直接写出S关于t的函数关系式;
③当线段A′C′与射线BB1有公共点时,求t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将正整数1至2018按一定规律排列如下表:
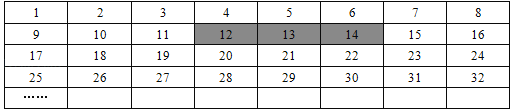
平移表中带阴影的方框,方框中三个数的和可能是( )
A. 2019 B. 2018 C. 2016 D. 2013
-
科目: 来源: 题型:
查看答案和解析>>【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
-
科目: 来源: 题型:
查看答案和解析>>【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.
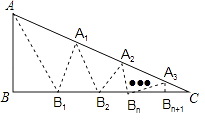
(1)若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(2)若一个三角形的最小角是4°,且该三角形的三个角均是此三角形的好角.请写出符合要求三角形的另两个角的度数 . (写出一种即可)
相关试题

