【题目】如图,平面直角坐标系中,菱形OABC的边OA在x轴正半轴上,OA=10,cos∠COA=![]() .一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
.一个动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,过点P作PQ⊥OA,交折线段OC﹣CB于点Q,以PQ为边向右作正方形PQMN,点N在射线OA上,当P点到达A点时,运动结束.设点P的运动时间为t秒(t>0).
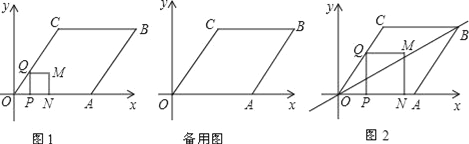
(1)C点的坐标为 ,当t= 时N点与A点重合;
(2)在整个运动过程中,设正方形PQMN与菱形OABC的重合部分面积为S,直接写出S与t之间的函数关系式和相应的自变量t的取值范围;
(3)如图2,在运动过程中,过点O和点B的直线将正方形PQMN分成了两部分,请问是否存在某一时刻,使得被分成的两部分中有一部分的面积是菱形面积的![]() ?若存在,请求出对应的t的值;若不存在,请说明理由.
?若存在,请求出对应的t的值;若不存在,请说明理由.
参考答案:
【答案】(1)t=![]() 时,N点与A点重合;(2)①
时,N点与A点重合;(2)①![]() ,
,
②![]() ,
,
③![]() ,
,
④8<t≤10,S=104﹣8t;
(3)①当0<t≤6,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
②当6<t≤8,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,t=0(舍),
,t=0(舍),
若![]() ,则
,则![]() ,t3=8;
,t3=8;
③8<t≤10,不存在符合条件的t值.
【解析】试题分析:(1)根据菱形的性质得出OA=OC,再根据三角函数求出点C的坐标即可;
(2)根据面积公式列出函数关系式,注意动点运动时的几种情况,得出自变量的取值范围;
(3)根据被分成的两部分中有一部分的面积是菱形面积的![]() ,画出图示,分几种情况进行讨论解答.
,画出图示,分几种情况进行讨论解答.
试题解析:(1)∵菱形OABC中,OA=10,
∴OC=10,
∵cos∠COA=![]() ,
,
∴点C的坐标为:(6,8),
∵动点P从点O出发,以每秒1个单位长度的速度沿线段OA方向运动,
∵OA=10,
∴t=![]() 时,N点与A点重合;
时,N点与A点重合;
(2)①![]() ,
,
②![]() ,
,
③![]() ,
,
④8<t≤10,S=104﹣8t;
(3)S菱形=80,直线OB过原点(0,0),B点(16,8),故直线OB解析式为![]() ,
,
直线OB与PQ、MN分别交于E、F点,如图:
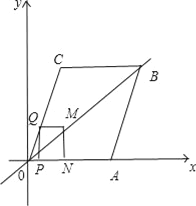
①当0<t≤6,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
②当6<t≤8,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,t=0(舍),
,t=0(舍),
若![]() ,则
,则![]() ,t3=8;
,t3=8;
③8<t≤10,不存在符合条件的t值.
-
科目: 来源: 题型:
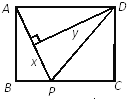
查看答案和解析>>【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数关系的大致图像是( )
A.
 B.
B. 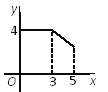 C.
C. 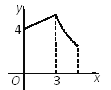 D.
D. 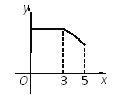
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列哪种光线形成的投影不是中心投影( )
A.探照灯
B.太阳
C.手电筒
D.路灯 -
科目: 来源: 题型:
查看答案和解析>>【题目】 2014年巴西世界杯足球赛正在如火如荼的进行,小明和喜爱足球的伙伴们一起预测“巴西队”能否获得本届杯赛的冠军,他们分别在3月、4月、5月、6月进行了四次预测,并且每次参加预测的人数相同,小明根据四次预测结果绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
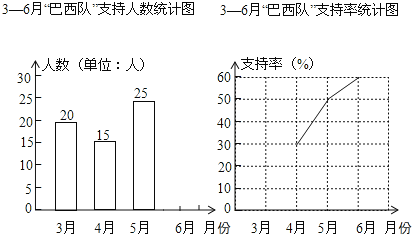
(1)每次有 人参加预测;
(2)计算6月份预测“巴西队”夺冠的人数;
(3)补全条形统计图和折线统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
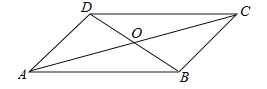
A.AB∥DC,AD∥BC
B.AB∥DC,∠A=∠C
C.AO=BO,CO=DO
D.∠A=∠C,∠B=∠D -
科目: 来源: 题型:
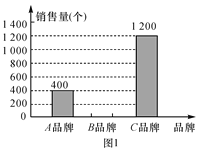
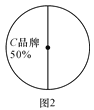
查看答案和解析>>【题目】端午节即将来临,某商场对去年端午节这天销售A,B,C三种品牌粽子的情况进行了统计,绘制如图1和图2所示的统计图.根据图中信息解答下列问题:
(1)哪一种品牌的粽子的销售量最大?
(2)补全图1中的条形统计图;
(3)写出A种品牌粽子在图2中所对应的圆心角的度数;
(4)根据上述统计信息,今年端午节期间该商场对A、B、C三种品牌的粽子如何进货?请你提一条合理化的建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB=DC,AD=BC
B.AB∥DC,AO=BO
C.AB=DC,∠B=∠D
D.AB∥DC,∠B=∠D
相关试题

