【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
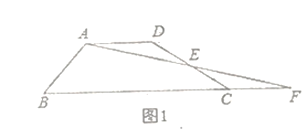
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
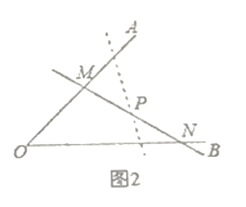
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
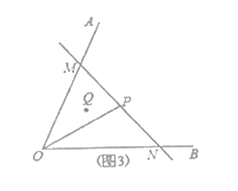
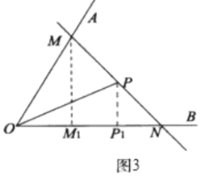
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
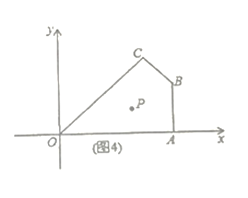
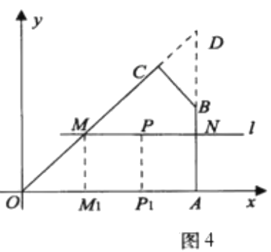
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
参考答案:
【答案】(1)证明见解析;(2)当直线旋转到点![]() 是
是![]() 的中点时
的中点时![]() 最小;(3)
最小;(3)![]() ;(4)10.
;(4)10.
【解析】
(1)根据可以求得△ADE≌△FCE,就可以得出S△ADE=S△FCE就可以得出结论;
(2)根据问题情境的结论可以得出当直线旋转到点P是MN的中点时S△MON最小,过点M作MG∥OB交EF于G.由全等三角形的性质可以得出结论;
(3)如图3,作PP1⊥OB,MM1⊥OB,垂足分别为P1,M1,再根据条件由三角函数值就可以求出结论;
(4)分情况讨论当过点P的直线l与四边形OABC的一组对边OC、AB分别交于点M、N,延长OC、AB交于点D,由条件可以得出AD=6,就可以求出△OAD的面积,再根据问题迁移的结论就可以求出最大值;
当过点P的直线l与四边形OABC的另一组对边CB、OA分别交M、N,延长CB交x轴于T,由B、C的坐标可得直线BC的解析式,就可以求出T的坐标,从而求出△OCT的面积,再由问题迁移的结论可以求出最大值,通过比较就可以求出结论.
(1)证明:![]() ,
,
![]()
![]() 点
点![]() 为
为![]() 边的中点,
边的中点,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
即![]()
(2)当直线旋转到点![]() 是
是![]() 的中点时,
的中点时,![]() 最小,如图2,
最小,如图2,

过点![]() 的另一条直线
的另一条直线![]() 交
交![]() 于点
于点![]() ,
,
设![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
由问题情境可以得出当![]() 是
是![]() 的中点时.
的中点时.![]()
![]() ,
,
![]() ,
,
![]() 当点
当点![]() 是
是![]() 的中点时,
的中点时,![]() 最小
最小
(3)如图3,作![]() ,垂足分别为
,垂足分别为![]() ,
,
在![]() 中,
中,
![]() ,
,
![]() .
.
由问题迁移的结论知道,
当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() .
.
在![]() 中,
中,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
(4)①如图4,当过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 的一组对边
的一组对边![]() 分别交于点
分别交于点![]() ,延长
,延长![]() 交于点
交于点![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
由问题迁移的结论可知,当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() 四边形
四边形![]() 的面积最大.
的面积最大.
作![]() 垂足分别为
垂足分别为![]() ,
,
![]()
![]() 点
点![]() 为
为![]() 中点
中点
![]() ,
,
![]()
![]()
②如图5,当过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 的另一组对
的另一组对![]() 边分别交
边分别交![]() 延长
延长![]() 交
交![]() 轴于
轴于![]() ,
,

![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,由题意,得
,由题意,得
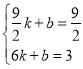 ,解得
,解得![]()
![]() ,
,
当![]() 时,
时,![]() ,
,
![]()
![]()
由问题迁移的结论可知,当![]() 时,
时,![]() 的面积最小,
的面积最小,
![]() 四边形
四边形![]() 的面积最大.
的面积最大.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述:截得四边形面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
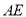 平分
平分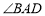 ,交
,交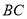 于点
于点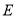 ,
,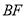 平分
平分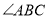 ,交
,交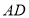 于点
于点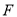 ,
,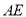 与
与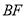 交于点
交于点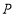 ,连接
,连接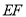 ,
,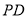 .
.(1)求证:四边形
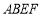 是菱形;
是菱形;(2)若
 ,
,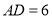 ,
,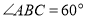 ,求
,求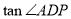 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,函数
 的图象与一次函数y=kx-k的图象的交点为A(m,2).
的图象与一次函数y=kx-k的图象的交点为A(m,2).(1)求一次函数的解析式;
(2)设一次函数y=kx-k的图象与y轴交于点B,若P是x轴上一点, 且满足△PAB的面积是4,
直接写出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件
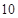 元,出厂价为每件
元,出厂价为每件 元,每月销售量
元,每月销售量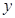 (件)与销售单价
(件)与销售单价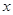 (元)之间的关系近似满足一次函数:
(元)之间的关系近似满足一次函数: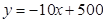 .
.(1)李明在开始创业的第一个月将销售单价定为
 元,那么政府这个月为他承担的总差价为多少元?
元,那么政府这个月为他承担的总差价为多少元?(2)设李明获得的利润为
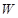 (元),当销售单价定为多少元时,每月可获得最大利润?
(元),当销售单价定为多少元时,每月可获得最大利润?(3)物价部门规定,这种节能灯的销售单价不得高于
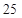 元.如果李明想要每月获得的利润不低于
元.如果李明想要每月获得的利润不低于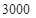 元,那么政府为他承担的总差价最少为多少元?
元,那么政府为他承担的总差价最少为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD的边长为4cm,∠A=120°,则菱形ABCD的面积为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学报名参加校运动会,有以下4个项目可供选择:径赛项目:100m,200m(分别用A1、A2表示).田赛项目:跳远,跳高(分用B1,B2表示).
(1)该同学从4个项目中任选一个,恰好是田赛项目的概率为 .
(2)该同学从4个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率 .
相关试题

