【题目】为保护环境,我市某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
参考答案:
【答案】(1)A型100万元,B型150万元;(2)三种方案,A型6辆,B型4辆;A型7辆,B型3辆;A型8辆,B型2辆;(3)A型8辆,B型2辆,费用最少,最少费用为1100万元
【解析】
(1)根据“购买A型公交车1辆,B型公交车2辆,共需400万元;购买A型公交车3辆,B型公交车2辆,共需600万元”, 分别设购买A型公交车每辆需x万元, 购买B型公交车每辆需y万元, 列二元一次方程组![]() 求解即可;
求解即可;
(2)设购买A型公交车a辆, 则B型公交车(10- a)辆, 列出不等式组 ,求出a的取值范围6≤a≤8;因此,符合条件的A型公交车的a可为6、7、8,而相对应的B型公交车可为4、3、2,所以一共有三种方案;
,求出a的取值范围6≤a≤8;因此,符合条件的A型公交车的a可为6、7、8,而相对应的B型公交车可为4、3、2,所以一共有三种方案;
(3)在(2)所求的三种方案的基础上,分别进行各个方案的总费用计算,通过比较,即可得出购买A型公交车8辆, 则B型公交车2辆总费用最少,最少为1100万元.
解: (1)设购买A型公交车每辆需x万元, 购买B型公交车每辆需y万元,由题意得:
![]()
解得![]()
答:购买A型公交车每辆需100万元, 购买B型公交车每辆需150万元.
(2)设购买A型公交车a辆, 则B型公交车(10- a)辆, 由题意得

解得: 6≤a≤8,
∴a=6,7, 8 ;
则(10-a) =4,3,2;
三种方案: 具体如下
①购买A型公交车6辆, 则B型公交车4辆;
②购买A型公交车7辆, 则B型公交车3辆;
③购买A型公交车8辆, 则B型公交车2辆;
(3)①购买A型公交车6辆, 则B型公交车4辆:
100×6+150×4= 1200万元;
②购买A型公交车7辆, 则B型公交车3辆:
100×7+150×3=1150万元;
③购买A型公交车8辆, 则B型公交车2辆:
100×8+150× 2= 1100万元;
故购买A型公交车8辆,则B型公交车2辆费用最少, 最少总费用为1100万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=130°,∠B=∠D=90°,点E,F分别是线段BC,DC上的动点.当△AEF的周长最小时,则∠EAF的度数为_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,
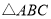 的顶点均在格点上,点A的坐标为
的顶点均在格点上,点A的坐标为 ,点B的坐标为
,点B的坐标为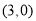 ,点C的坐标为
,点C的坐标为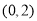 .
.
(1)以点C为旋转中心,将
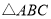 旋转
旋转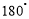 后得到
后得到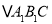 ,请画出
,请画出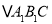 ;
;(2)平移
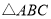 ,使点A的对应点
,使点A的对应点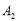 的坐标为
的坐标为 ,请画出
,请画出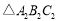 ;
;(3)若将
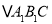 绕点P旋转可得到
绕点P旋转可得到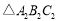 ,则点P的坐标为___________.
,则点P的坐标为___________. -
科目: 来源: 题型:
查看答案和解析>>【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所知道的四边形中是勾股四边形的两种图形的名称_____,_____;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE,连接AD、DC,若∠DCB=30°,试证明;DC2+BC2=AC2.(即四边形ABCD是勾股四边形)

-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:

(1)探究:
①数轴上表示7和1的两点之间的距离是_______.
②数轴上表示﹣2和﹣9的两点之间的距离是________.
(2)归纳:
一般的,数轴上表示数m和数n的两点之间的距离等于_______.
(3)应用:
①若数轴上表示数a的点位于﹣5与4之间,则|a+5|+|a﹣4|的值=________.
②若a表示数轴上的一个有理数,且|a-3|=| a+1|,则a =______.
③若a表示数轴上的一个有理数,且|a+5|+|a﹣4|>9,则有理数a的取值范围是______.
(4)拓展:
已知,如图A、B分别为数轴上的两点,A点对应的数为-10,B点对应的数为70.若当电子蚂蚁P从A点出发,以3个单位/秒的速度向右运动,同时另一只电子蚂蚁Q恰好从B点出发,以2单位/秒的速度向左运动,求经过多长时间两只电子蚂蚁在数轴上相距35个单位长度,并写出此时点P所表示的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
相关试题

