Question

【题目】如图，在平行四边形BFEC中，连接FC，并延长至点D，延长CF至点A，使DC＝AF，连接AB、DE．

（1）求证：AB∥DE．

（2）若平行四边形BFEC是菱形，且∠ABC＝90°，AB＝4，BC＝3，则CF＝　 　．

Answer 1

【答案】（1）见解析；（2）3.6

【解析】

（1）根据平行四边形的性质得到BF∥CE，BF=CE，根据平行线的性质得到∠BFC=∠ECF，由平角的定义得到∠BFA=∠ECD，根据全等三角形的性质得到∠A=∠D，根据平行线的判定即可得到结论；

（2）过点B作BM⊥CF于点M，根据勾股定理得到AC==5，根据三角形的面积公式得到BM==2.4，根据菱形的性质得到BF=BC=3，CF=2FM，根据勾股定理即可得到结论．

（1）证明：∵四边形BFEC为平行四边形，

∴BF∥CE，BF＝CE，

∴∠BFC＝∠ECF，

∴∠BFA＝∠ECD，

在△AFB与△DCE中，，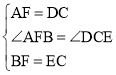

∴△AFB≌△DCE，（SAS），

∴∠A＝∠D，

∴AB∥DE；

（2）解：过点B作BM⊥CF于点M，

在Rt△ABC中，AC＝＝5，

∵S△ABC＝ABBC＝ACBM，

∴BM＝＝2.4，

又∵四边形BFEC为菱形，

∴BF＝BC＝3，CF＝2FM，

在Rt△BFM中，FM＝＝1.8，

∴CF＝2×1.8＝3.6．

故答案为：3.6．