【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
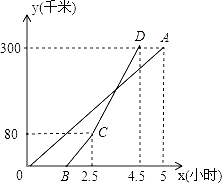
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
参考答案:
【答案】(1)轿车到达乙地后,货车距乙地30千米;
【解析】
试题分析:(1)根据图象可知货车5小时行驶300千米,由此求出货车的速度为60千米/时,再根据图象得出货车出发后4.5小时轿车到达乙地,由此求出轿车到达乙地时,货车行驶的路程为270千米,而甲、乙两地相距300千米,则此时货车距乙地的路程为:300-270=30千米;
(2)设CD段的函数解析式为y=kx+b,将C(2.5,80),D(4.5,300)两点的坐标代入,运用待定系数法即可求解;
(3)设货车从甲地出发x小时后再与轿车相遇,根据轿车(x-4.5)小时行驶的路程+货车x小时行驶的路程=300千米列出方程,解方程即可.
试题解析:(1)根据图象信息:货车的速度V货=![]() =60(千米/时).
=60(千米/时).
∵轿车到达乙地的时间为货车出发后4.5小时,
∴轿车到达乙地时,货车行驶的路程为:4.5×60=270(千米),
此时,货车距乙地的路程为:300-270=30(千米).
答:轿车到达乙地后,货车距乙地30千米;
(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).
∵C(2.5,80),D(4.5,300)在其图象上,
∴![]() ,解得
,解得![]() ,
,
∴CD段函数解析式:y=110x-195(2.5≤x≤4.5);
(3)设货车从甲地出发后x小时后再与轿车相遇.
∵V货车=60千米/时,V轿车=![]() =110(千米/时),
=110(千米/时),
∴110(x-4.5)+60x=300,
解得x≈4.68(小时).
答:货车从甲地出发约4.68小时后再与轿车相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了城市绿化建设,某中学初三(2)班计划组织部分同学义务植树180棵,由于同学们参与的积极性很高,实际参加植树活动的人数比原计划增加了
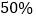 ,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?
,结果每人比原计划少栽了2棵树,问实际有多少人参加了这次植树活动?(1)小明设原计划有
 人参加植树活动,请你完成他的求解过程;
人参加植树活动,请你完成他的求解过程;(2)小红设原计划每人栽
 棵树,则由题意可得方程为: .(不需要求解)
棵树,则由题意可得方程为: .(不需要求解) -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC为等边三角形,边长为a,DF⊥AB.EF⊥AC
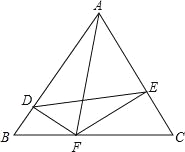
(1)求证:△BDF∽△CEF;
(2)若a=4,设BF=m,四边形ADFE面积为S,求出S与m之间的函数关系式,并探究当m为何值时S取最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】

A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的两条边长是2和5,则第三条边a取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=kx+b与y=2x+1平行,且经过点(﹣3,4),则函数y=kx+b的图象可以看作由函数y=2x+1的图象向上平移_____个单位长度得到的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如下图, AB∥CD,点E,F分别为AB,CD上一点.
(1) 在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.

(2)如下图,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).
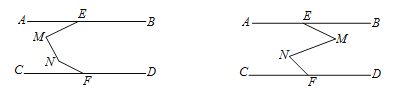
相关试题

