搜索
【题目】阅读材料：求1＋2＋22＋23＋24＋…＋22017的值.
解：设S＝1＋2＋22＋23＋24＋…＋22017，
将等式两边同时乘以2得，2S＝2＋22＋23＋24＋25＋…＋22017＋22018，
将下式减去上式得：2S－S＝22018－1，即S＝22018－1，
所以1＋2＋22＋23＋24＋…＋2201722018－1，
请你依照此法计算：
（1）1＋2＋22＋23＋24＋…＋29；
（2）1＋5＋52＋53＋54＋…＋5n（其中n为正整数）.
参考答案：
【答案】（1）210－1；（2）P＝
【解析】试题分析：（1）设原式=S，两边乘以2变形后，相减求出S即可；
（2）设原式=S，两边乘以5变形后，相减求出S即可．
试题解析：解：（1）设S=1+2+22+…+29，
两边乘以2得：2S=2+22+…+210，
两式相减得：2S-S=S=210－1.
（2）设P＝1＋5＋52＋53＋……＋5n；
将两边同时乘以5得，5P＝1＋5＋52＋53＋…＋5n＋5n＋1；
下式减去上式得：4P＝5n＋1－1
所以 P＝
所以1＋5＋52＋53＋…＋5n＝
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．
（
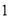）可求得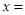
__________，第
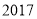个格子中的数为__________．（
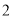）判断：前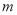
个格子中所填整数之和是否可能为
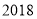？若能，求出
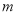的值，若不能，请说明理由．（
）若取前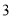
格子中的任意两个数记作
、
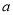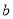，且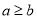
，那么所有的
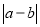的和可以通过计算
得到，其结果为__________；若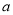
、
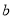为前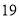
格子中的任意两个数记作
、
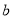，且
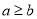，则所有的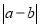
的和为__________．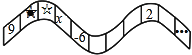
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的个数是（ ）
①对顶角相等；
②等角的补角相等；
③两直线平行，同旁内角相等；
④在同一平面内，过一点有且只有一条直线与已知直线垂直
A.1B.2C.3D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：
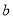是最小的正整数，且
、
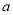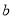满足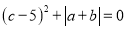
，请回答问题：（
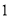）请直接写出
、
、
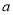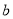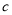的值： 
__________， 
__________， 
__________．（
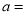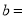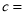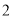）数轴上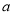
， 
， 
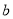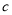所对应的点分别为
， 
， 
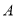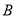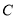，点
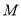是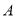
， 
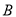之间的一个动点，其对应的数为
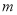，请化简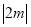
（请写出化简过程）．（
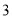）在（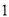
）、（
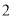）的条件下，点
、
、
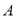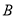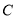开始在数轴上运动，若点
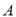以每秒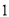
个单位长度的速度向左运动．同时，点
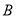和点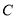
分别以每秒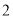
个单位长度和
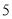个单位长度的速度向右运动，假设
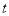秒钟过后，若点
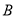与点
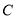之间的距离表示为
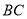，点
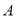与点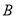
之间的距离表示为
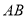．请问： 
的值是否随着时间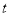
的变化而改变？若变化，请说明理由；若不变，请求其值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y＝ax2＋bx＋c经过A（－4，3）、B（2，0）两点，当x=3和x=－3时，这条抛物线上对应点的纵坐标相等．经过点C（0，－2）的直线l与 x轴平行，O为坐标原点．
（1）求直线AB和这条抛物线的解析式；
（2）以A为圆心，AO为半径的圆记为⊙A，判断直线l与⊙A的位置关系，并说明理由；
（3）设直线AB上的点D的横坐标为－1，P（m，n）是抛物线y＝ax2＋bx＋c上的动点，当△PDO的周长最小时，求四边形CODP的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知数轴上三点A，O，B表示的数分别为6，0，－4，动点P从A出发，以每秒6个单位的速度沿数轴向左匀速运动.
（1）当点P到点A的距离与点P到点B的距离相等时，点P在数轴上表示的数是 ；
（2）另一动点R从B出发，以每秒4个单位的速度沿数轴向左匀速运动，若点P、R同时出发，问点P运动多少时间追上点R？
（3）若M为AP的中点，N为PB的中点，点P在运动过程中，线段MN的长度是否发生变化？若发生变化，请你说明理由；若不变，请你画出图形，并求出线段MN的长度.
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了调查瑞州市2016年初三年级学生的身高，从中抽取出200名学生进行调查，这个问题中样本容量为（ ）
A.被抽取的200名学生的身高
B.200
C.200名
D.初三年级学生的身高
相关试题
