【题目】台风是一种自然灾害,它以台风中心为圆心,在周围数十千米范围内形成气旋风暴,有极强的破坏力.今年首个超强台风“圣帕”第0709号超强台风于8月13日在北纬21.3度,东经123.3度的太平洋上生成,其中心气压925百帕,近中心最大风速55米/秒,生成时还是热带风暴的“圣帕”,在连跳两级后,15日晚8时已“变身”为超强台风.向台湾东部沿海逼近并登陆台湾岛,之后于19日上午将在福建中南部沿海福州一带再次登陆.在这之前,台风中心在我国台湾海峡的B处,在沿海城市福州A的正南方向240千米,其中心风力为12级,每远离台风中心25千米,台风就会减弱一级,如图所示,该台风中心正以20千米/时的速度沿北偏东30°方向向C移动,且台风中心的风力不变,若城市所受风力达到或超过4级,则称受台风影响.试问: 
(1)该城市是否会受到台风影响?请说明理由.
(2)若会受到台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
参考答案:
【答案】
(1)解:该城市会受到台风影响.
理由:如图1,
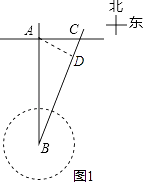
过点A作AD⊥BC于D点,则AD即为该城市距离台风中心的最短距离.
在Rt△ABD中,因为∠B=30°,AB=240.
AD= ![]() ×240=120(千米).
×240=120(千米).
由题可知,距台风中心在(12﹣4)×25=200(千米)以内时,则会受到台风影响.
因为120千米<200千米,因此该城市将会受到“圣帕”影响
(2)解:依题(1)可知,当点A距台风中心不超过200千米时,会受台风影响,
故在BC上作AE=AF=200;
台风中心从点E移动到点F处时,
该城市会处在台风影响范围之内.(如图2)
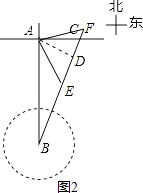
DE=160(千米).
所以EF=2×160=320(千米).
又知“圣帕”中心以20千米/时的速度移动.
所以台风影响该城市320÷20=16(小时)
(3)解:∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(120÷25)=7.2(级).
答:该城市受台风影响最大风力7.2级
【解析】(1)过点A作AD⊥BC于D点,求出AD的长,比较即可得到答案;(2)根据题意找出点E和点F,根据勾股定理求出EF的长,根据台风的速度求出时间;(3)根据每远离台风中心25千米,台风就会减弱一级计算即可.
【考点精析】认真审题,首先需要了解关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.

(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】近两年,市区的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

-
科目: 来源: 题型:
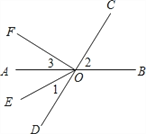
查看答案和解析>>【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=130°36′,那么根据 ,可得∠BOD= °;
(3)如果∠1与∠3的度数之比为3:4,求∠EOC和∠2的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 垂直于同一直线的两条直线平行
B. 有两边和其中一边上的高对应相等的两个三角形全等
C. 三角形三个内角中,至少有2个锐角
D. 有两条边和一个角对应相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( )

A. b2>4ac
B. ax2+bx+c≥﹣6
C. 若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
D. 关于x的一元二次方程ax2+bx+c=﹣4的两根为﹣5和﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组数是三角形的三边,能组成直角三角形的一组数是( )
A.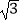 ,
, 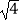 ,
, 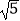

B.2,3,4
C.3,4,5
D.6,8,12
相关试题

