【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0),C(﹣1,0).
(1)将△ABC向右平移5个单位,再向下平移4个单位得△A1B1C1,图中画出△A1B1C1,平移后点A的对应点A1的坐标是______.
(2)将△ABC沿x轴翻折△A2BC,图中画出△A2BC,翻折后点A对应点A2坐标是______.
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为______.

参考答案:
【答案】(1)画图见解析,A1的坐标:(3,﹣1);
(2)画图见解析,A2坐标:(﹣2,﹣3);
(3)△ABC扫过的面积为:13.5.
【解析】试题分析:(1)直接利用平移的性质得出对应点位置进而得出答案;
(2)利用关于x轴对称点的性质进而得出对应点位置;
(3)利用平移的性质可得△ABC扫过的面积为△A′B′C′+平行四边形A′C′CA的面积.
试题解析:(1)如图所示:△A1B1C1,即为所求,
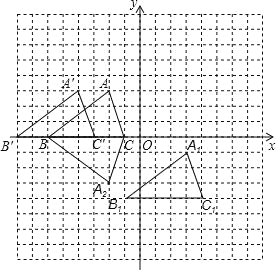
平移后点A的对应点A1的坐标是:(3,﹣1);
故答案为:(3,﹣1);
(2)如图所示:△A2BC,即为所求,翻折后点A对应点A2坐标是:(﹣2,﹣3);
故答案为:(﹣2,﹣3);
(3)将△ABC向左平移2个单位,则△ABC扫过的面积为:
S△A′B′C′+S平行四边形A′C′CA=![]() ×3×5+2×3=13.5.
×3×5+2×3=13.5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示,在直角梯形ABCD中,∠BAD=90°,E是直线AB上一点,过E作直线
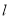 //BC,交直线CD于点F.将直线
//BC,交直线CD于点F.将直线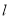 向右平移,设平移距离BE为
向右平移,设平移距离BE为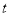 (t
(t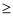 0),直角梯形ABCD被直线
0),直角梯形ABCD被直线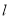 扫过的面积(图中阴影部份)为S,S关于
扫过的面积(图中阴影部份)为S,S关于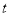 的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.
的函数图象如图②所示,OM为线段,MN为抛物线的一部分,NQ为射线,N点横坐标为4.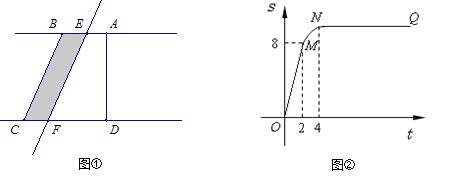
信息读取
(1)梯形上底的长AB= ;(2) 直角梯形ABCD的面积= ;
图象理解
(3)写出图②中射线NQ表示的实际意义;(4) 当
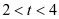 时,求S关于
时,求S关于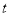 的函数关系式;
的函数关系式;问题解决
(5)当t为何值时,直线l将直角梯形ABCD分成的两部分面积之比为1: 3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若∠A=35°,∠B=65°,则∠C的度数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一串有理数按下列规律排列,解答下列问题:
(1)在A处的数是正数还是负数?
(2)负数排在A,B,C,D中的什么位置?
(3)第2 018个数是正数还是负数?排在对应于A,B,C,D中的什么位置?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某水库一周内水位高低的变化情况(用正数记水位比前一日上升数,用负数记下降数).那么本周星期几水位最低( )
星期
一
二
三
四
五
六
日
水位变化/米
0.12
﹣0.02
﹣0.13
﹣0.20
﹣0.08
﹣0.02
0.32
A. 星期二 B. 星期四 C. 星期六 D. 星期五
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形,其每个内角都是140°,则该多边形的边数是( )
A.6B.7C.8D.9
-
科目: 来源: 题型:
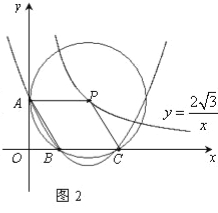
查看答案和解析>>【题目】在直角坐标系
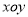 中,已知点P是反比例函数
中,已知点P是反比例函数 (
(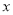 >0)图象上一个动点,以P为圆心的圆始终与
>0)图象上一个动点,以P为圆心的圆始终与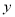 轴相切,设切点为A.
轴相切,设切点为A.(1)如图1,⊙P运动到与
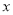 轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.
轴相切,设切点为K,试判断四边形OKPA的形状,并说明理由.(2)如图2,⊙P运动到与
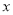 轴相交,设交点为B,C.当四边形ABCP是菱形时:
轴相交,设交点为B,C.当四边形ABCP是菱形时:①求出点A,B,C的坐标.
②在过A,B,C三点的抛物线上是否存在点M,使△MBP的面积是菱形ABCP面积的
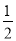 .若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
.若存在,试求出所有满足条件的M点的坐标,若不存在,试说明理由.
相关试题

