【题目】据电力部门统计,每天8:00至21:00是用电的高峰期,简称“峰时”,21:00至次日8:00是用电的低谷时期,简称“谷时”,为了缓解供电需求紧张矛盾,某市电力部门于本月初统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
时间 | 换表前 | 换表后 | |
峰时(8:00~21:00) | 谷时(21:00~次日8:00) | ||
电价 | 每度0.52元 | 每度0.55元 | 每度0.30元 |
(1)小张家上月“峰时”用电50度,“谷时”用电20度,若上月初换表,则相对于换表前小张家的电费是增多了还是减少了?增多或减少了多少元?请说明理由.
(2)小张家这个月用电95度,经测算比换表前使用95度电节省了5.9元,问小张家这个月使用“峰时电”和“谷时电”分别是多少度?(12分)
参考答案:
【答案】(1)节省2.9元,理由见解析;(2)“峰时电”60度,“谷时电”35度.
【解析】
试题分析:(1)分别求出换表前和换表后的电费,然后再进行比较大小,得出答案;(2)首先设小张家这个月使用“峰时电”是x度,则“谷时电”为(95-x)度,然后根据题意列出方程,从而求出x的值,得到答案.
试题解析:(1)换表前:0.52×(50+20)=36.4(元) 换表后:0.55×50+0.30×20=33.5(元)
33.5-36.4=-2.9(元) ∴若上月初换表,则相对于换表前小张家的电费节省了2.9元.
(2)设小张家这个月使用“峰时电”是x度,则“谷时电”为(95-x)度,
由题意可得方程![]() ,解之得x=60,95-60=35,
,解之得x=60,95-60=35,
即小张家这个月使用“峰时电”60度,“谷时电”35度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一种单价为
 元的篮球,如果以单价
元的篮球,如果以单价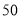 元售出,那么每天可售出50个.根据销售经验,售价每提高
元售出,那么每天可售出50个.根据销售经验,售价每提高 元.销售量相应减少1个。
元.销售量相应减少1个。(1)假设销售单价提高
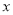 元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。
元,那么销售每个篮球所获得的利润是_____元;这种篮球每天的销售量是_________个。(2)假设每天销售这种篮球所得利润为y ,请用含
 的代数式表示y。
的代数式表示y。(3)假如你是商场老板,为了在出售这种篮球时获得最大利润,你该提高多少元?最大利润是多少?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.实验数据记录如下表:
x(cm)
10
15
20
25
30
y(g)
30
20
15
12
10
(1)猜测y与x之间的函数关系,求出函数关系式并加以验证;
(2)当砝码的质量为24g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?

-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高度发展,据调查,长沙市某家小型“大学生自主创业”的快递公司,今年三月份与五月份完成投递的快递总件数分别为10万件和12.1万件,现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递总件数的月平均增长率;
(2)如果平均每人每月最多可投递0.6万件,那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E。
(1)∠B= 度.
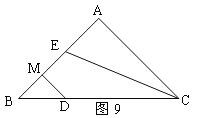
(2)如图9,若点D在斜边BC上,DM垂直平分BE,垂足为M。求证:BD=AE;
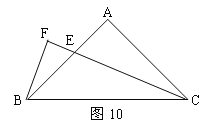
(3)如图10,过点B作BF⊥CE,交CE的延长线与点F。若CE=6,求△BEC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
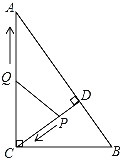
(1)求线段CD的长;
(2)当t为何值时,△CPQ与△ABC相似?
(3)当t为何值时,△CPQ为等腰三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图,解答下列问题.

(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,……,第六层有11个圆圈.如果要你继续画下去第n层 有 圆圈
(2)某一层上有65个圆圈,这是第 层
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22,
由此得,1+3 = 22.
同样,
由前三层的圆圈个数和得:1+3+5 = 32.
由前四层的圆圈个数和得:1+3+5+7 = 42.
由前五层的圆圈个数和得:1+3+5+7+9 = 52.
……
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+299的和;
(5)计算:101+103+105+…+299的和.
相关试题

