【题目】如图1,某商场有一双向运行的自动扶梯,扶梯上行和下行的速度保持不变且相同,甲、乙两人同时站上了此扶梯的上行和下行端,甲站上上行扶梯的同时又以0.8m/s的速度往上跑,乙站上下行扶梯后则站立不动随扶梯下行,两人在途中相遇,甲到达扶梯顶端后立即乘坐下行扶梯,同时以0.8m/s的速度往下跑,而乙到达底端后则在原地等候甲.图2中线段OB、AB分别表示甲、乙两人在乘坐扶梯过程中,离扶梯底端的路程y(m)与所用时间x(s)之间的部分函数关系,结合图象解答下列问题: 
(1)求点B的坐标;
(2)求AB所在直线的函数表达式;
(3)乙到达扶梯底端后,还需等待多长时间,甲才到达扶梯底端?
参考答案:
【答案】
(1)解:设扶梯上行和下行的速度为xm/s,则
7.5(2x+0.8)=30,
解得x=1.6,
7.5(x+0.8)=7.5×(1.6+0.8)=7.5×2.4=18.
则点B的坐标是 (7.5,18).
答:B(7.5,18)
(2)解:设直线AB的函数关系式为y=kx+b,
点A、B坐标分别为(0,30),(7.5,18)代入:y=kx+b,得:
![]() ,
,
解得: ![]() .
.
故AB所在直线的函数关系式为y=﹣1.6x+30
(3)解:由题意,得
30×2÷(1.6+0.8)﹣30÷1.6
=60÷2.4﹣18.75
=25﹣18.75
=6.25(s).
故乙到达扶梯底端后,还需等待6.25s,甲才到达扶梯底端
【解析】(1)可设扶梯上行和下行的速度为xm/s,根据相遇时路程和为30,可列方程7.5(2x+0.8)=30,求得扶梯上行和下行的速度,从而求解;(2)设出一次函数的一般形式,将A、B两点坐标,代入求得直线AB的函数关系式;(3)分别求得甲、乙两人所花的时间,相减即可求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
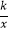 (x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则t的值是( )
A.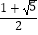
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.
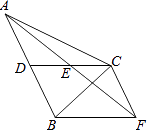
(1)求证:CF=AD;
(2)若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战初三物理、化学实验操作考试,某校对初三学生进行了模拟训练,物理、化学各有4各不同的操作实验题目,物理用番号①、②、③、④代表,化学用字母a、b、c、d表示,测试时每名学生每科只操作一个实验,实验的题目由学生抽签确定,第一次抽签确定物理实验题目,第二次抽签确定化学实验题目.
(1)请用树形图法或列表法,表示某个同学抽签的各种可能情况.
(2)小张同学对物理的①、②和化学的b、c号实验准备得较好,他同时抽到两科都准备的较好的实验题目的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】国家环保局统一规定,空气质量分为5级.当空气污染指数达0﹣50时为1级,质量为优;51﹣100时为2级,质量为良;101﹣200时为3级,轻度污染;201﹣300时为4级,中度污染;300以上时为5级,重度污染.泰州市环保局随机抽取了2015年某些天的空气质量检测结果,并整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
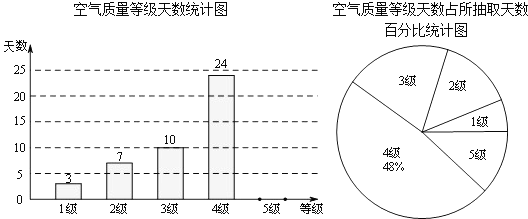
(1)本次调查共抽取了天的空气质量检测结果进行统计;
(2)补全条形统计图;
(3)扇形统计图中3级空气质量所对应的圆心角为°;
(4)如果空气污染达到中度污染或者以上,将不适宜进行户外活动,根据目前的统计,请你估计2015年该城市有多少天不适宜开展户外活动.(2015年共365天) -
科目: 来源: 题型:
查看答案和解析>>【题目】某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.

(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长.
(2)如图3,当∠BAC=12°,求AD的长(结果保留根号).
[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]
-
科目: 来源: 题型:
查看答案和解析>>【题目】小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是,车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中 ②的位置).例如,图2是某巷子的俯视图,巷子路面宽4m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.

(1)小平认为长8m,宽3m的消防车不能通过该直角转弯,请你帮他说明理由;
(2)小平提出将拐弯处改为圆弧( 和
和  是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
是以O为圆心,分别以OM和ON为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子?
相关试题

