【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.其中正确的结论的个数是( )
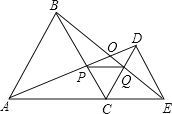
A.2个 B.3个 C.4个 D.5个
参考答案:
【答案】C.
【解析】
试题分析:根据题意,结合图形,对选项一一求证,判定正确选项.(根据等边三角形的性质可证∠DCB=60°,由三角形内角和外角定理可证∠DPC>60°,所以DP≠DE)
解:①△ABC和△DCE均是等边三角形,点A,C,E在同一条直线上,
∴AC=BC,EC=DC,∠BCE=∠ACD=120°
∴△ACD≌△ECB
∴AD=BE,故本选项正确;
②∵△ACD≌△ECB
∴∠CBQ=∠CAP,
又∵∠PCQ=∠ACB=60°,CB=AC,
∴△BCQ≌△ACP,
∴CQ=CP,又∠PCQ=60°,
∴△PCQ为等边三角形,
∴∠QPC=60°=∠ACB,
∴PQ∥AE,故本选项正确;
③∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∴∠ACP=∠BCQ,
∵AC=BC,∠DAC=∠QBC,
∴△ACP≌△BCQ(ASA),
∴CP=CQ,AP=BQ,故本选项正确;
④已知△ABC、△DCE为正三角形,
故∠DCE=∠BCA=60°∠DCB=60°,
又因为∠DPC=∠DAC+∠BCA,∠BCA=60°∠DPC>60°,
故DP不等于DE,故本选项错误;
⑤∵△ABC、△DCE为正三角形,
∴∠ACB=∠DCE=60°,AC=BC,DC=EC,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
∴△ACD≌△BCE(SAS),
∴∠CAD=∠CBE,
∴∠AOB=∠CAD+∠CEB=∠CBE+∠CEB,
∵∠ACB=∠CBE+∠CEB=60°,
∴∠AOB=60°,
故本选项正确.
综上所述,正确的结论是①②③⑤.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )
A.相等 B.互补 C.相等或互补 D.相等且互补
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠1的对顶角是∠2,∠2的邻补角是∠3,且∠3=45°,则∠1=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB=DE,BF=CE。
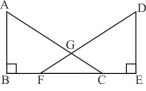
求证:(1)△ABC≌△DEF;
(2)GF=GC。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知不等式
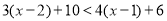 的最小整数解为方程
的最小整数解为方程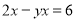 的解,求代数式
的解,求代数式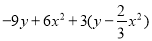 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 全等三角形是指形状相同的两个三角形
B. 全等三角形的周长和面积分别相等
C. 全等三角形是指面积相等的两个三角形
D. 所有的等边三角形都是全等三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.3x2﹣4x2=﹣1 B.3x+x=3x2
C.4xx=4x2 D.﹣4x6÷2x2=﹣2x3
相关试题

