搜索
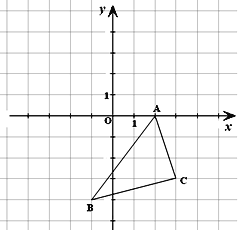
【题目】如图所示的直角坐标系中，解答下列问题：
（1）分别写出A、B两点的坐标；
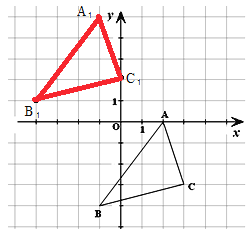
（2）将△ABC向左平移3个单位长度，再向上平移5个单位长度，画出平移后的△A1B1C1；
（3）求 △A1B1C1的面积。
参考答案：
【答案】（1）A（2,0） B（-1,-4）；（2）作图见解析；（3）
【解析】试题分析：（1）从直角坐标系中读出点的坐标．
（2）根据平移规律找出各点平移后后得到对应点，顺次连接即可．
（3）根据S△ABC=S长方形ADEF-S△ABD-S△EBC-S△ACF，即可求得三角形的面积．
试题解析：（1）A（2,0） B（-1,-4）
（2）如图，
（3）如图，
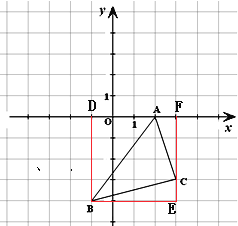
S△ABC=S长方形DBEF-S△ABD-S△EBC-S△ACF
=4×4-
×4×1-
×3×1-
×4×3=
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一拱形公路桥，圆弧形桥拱的水面跨度AB＝80 m，桥拱到水面的最大高度为20 m.(1)求桥拱的半径．
(2)现有一艘宽60 m，顶部截面为长方形且高出水面9 m的轮船要经过这座拱桥，这艘轮船能顺利通过吗？请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列7个事件中：（1）掷一枚硬币，正面朝上．（2）从一副没有大小王的扑克牌中抽出一张恰为黑桃．（3）随意翻开一本有400页的书，正好翻到第100页．（4）天上下雨，马路潮湿．（5）你能长到身高4米．（6）买奖券中特等大奖．（7）掷一枚正方体骰子，得到的点数＜7．其中（将序号填入题中的横线上即可）确定事件为________；不确定事件为________；不可能事件为________；必然事件为________；不确定事件中，发生可能性最大的是________，发生可能性最小的是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为弘扬中华传统文化，黔南州近期举办了中小学生“国学经典大赛”．比赛项目为：A．唐诗；B．宋词；C．论语；D．三字经．比赛形式分“单人组”和“双人组”．
（1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？
（2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少？请用画树状图或列表的方法进行说明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
（1）在图中画出与关于直线
成轴对称的△A′B′C′；（2）线段CC′被直线
；（3）△ABC的面积为 ；
（4）在直线
上找一点P，使PB+PC的长最短．
-
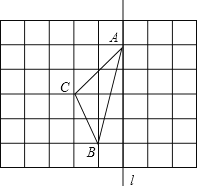
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P在y轴上，⊙P交x轴于A，B两点，连接BP并延长交⊙P于点C，过点C的直线y＝2x＋b交x轴于点D，且⊙P的半径为
，AB＝4.(1)求点B，P，C的坐标；(2)求证：CD是⊙P的切线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】投掷一枚质地均匀的正方体骰子．
（1）下列说法中正确的有 ． （填序号）
①向上一面点数为1点和3点的可能性一样大；
②投掷6次，向上一面点数为1点的一定会出现1次；
③连续投掷2次，向上一面的点数之和不可能等于13．
（2）如果小明连续投掷了10次，其中有3次出现向上一面点数为6点，这时小明说：投掷正方体骰子，向上一面点数为6点的概率是
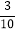． 你同意他的说法吗？说说你的理由．（3）为了估计投掷正方体骰子出现6点朝上的概率，小亮采用转盘来代替骰子做实验．下图是一个可以自由转动的转盘，请你将转盘分为2个扇形区域，分别涂上红、白两种颜色，使得转动转盘，当转盘停止转动后，指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同．（友情提醒：在转盘上用文字注明颜色和扇形圆心角的度数．）
相关试题
