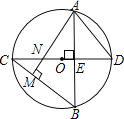
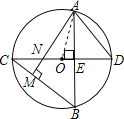
【题目】如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.
(1)求证:AD=AN;
(2)若AB=![]() ,ON=1,求⊙O的半径.
,ON=1,求⊙O的半径.
(3)若![]() 且AE=4,求CM
且AE=4,求CM
参考答案:
【答案】(1)、证明过程见解析;(2)、3;(3)、CM=2.
【解析】
试题分析:(1)、根据同弧所对的圆周角相等得出∠B=∠D,根据双垂直得出∠B=∠ANE,从而得出∠D=∠ANE,从而得到答案;(2)、设NE=x,则OE=x-1,ED=x,r=2x-1,根据Rt△AOE的勾股定理得出x的值,从而求出半径;(3)、根据△ANE的面积等于△ADE的面积以及S△CMN:S△AND=1:8,从而得出S△CMN:S△ANE=1:4,求出答案.
试题解析:(1)、根据图示可得:∠B=∠D ∵AM⊥BC,AB⊥CD ∴∠B=∠ANE
∴∠ANE=∠D ∴AD=AN
(2)、∵AB=![]() ,AE⊥CD,∴AE=
,AE⊥CD,∴AE=![]() ,又∵ON=1,∴设NE=x,则OE=x-1,NE=ED=x,
,又∵ON=1,∴设NE=x,则OE=x-1,NE=ED=x,
r=OD=OE+ED=2x-1 连结AO,则AO=OD=2x-1,
∵△AOE是直角三角形,AE=![]() ,OE=x-1,AO=2x-1, ∴
,OE=x-1,AO=2x-1, ∴![]()
解得x=2,∴r=2x-1=3.
(3)、∵AD=AN,AB⊥CD,∴AE平分ND,∴S△ANE=S△ADE ∵S△CMN:S△AND=1:8,∴S△CMN:S△ANE=1:4,
又∵△CMN∽△AEN,∴![]() ∵AE=4,∴CM=2
∵AE=4,∴CM=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(0,4).
(1)求此一次函数的解析式;
(2)当y=-5时求x的值;
(3)求此函数图象与两坐标轴所围成的三角形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离S(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据题目和图象所提供的信息,下列说法正确的是( )
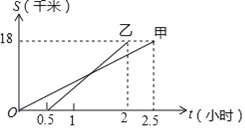
A. 乙比甲先到达B地
B. 乙在行驶过程中没有追上甲
C. 乙比甲早出发半小时
D. 甲的行驶速度比乙的行驶速度快
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组
(1)2x﹣3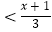
(2)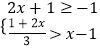 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(﹣3,3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=100°,沿BD对折恰使点A落在BC边上的E点,EC上有一点F,且DF=CF,(1)求证:DF=AD,(2) 猜想:BC与BD+AD的关系,并说明理由。
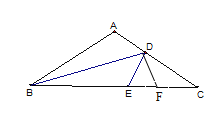
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级学生完成课题学习“从数据谈节水”后,积极践行“节约用水,从我做起”,现在从七年级400名学生中选出10名学生统计各自家庭一个月的节水情况如下表:
节水量(m3)
0.2
0.25
0.3
0.4
0.5
家庭数
1
2
2
4
1
那么这组数据的众数和平均数分别是( )
A. 0.4m3和0.34m3 B. 0.4m3和0.3m3 C. 0.25m3和0.34m3 D. 0.25m3和0.3m3
相关试题

