【题目】如图,ABCD中,点O是AC与BD的交点,过点O的直线与BA、DC的延长线分别交于点E、F. 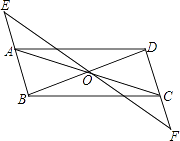
(1)求证:△AOE≌△COF;
(2)请连接EC、AF,则EF与AC满足什么条件时,四边形AECF是矩形,并说明理由.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AO=OC,AB∥CD.
∴∠E=∠F.
∵在△AOE与△COF中, 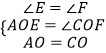 ,
,
∴△AOE≌△COF(AAS)
(2)连接EC、AF,
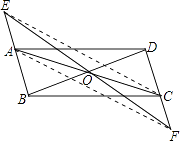
则EF与AC满足EF=AC时,四边形AECF是矩形,
理由如下:
由(1)可知△AOE≌△COF,
∴OE=OF,
∵AO=CO,
∴四边形AECF是平行四边形,
∵EF=AC,
∴四边形AECF是矩形.
【解析】(1)根据平行四边形的性质和全等三角形的证明方法证明即可;(2)请连接EC、AF,则EF与AC满足EF=AC时,四边形AECF是矩形,首先证明四边形AECF是平行四边形,再根据对角线相等的平行四边形为矩形即可证明.
【考点精析】利用平行四边形的性质和矩形的判定方法对题目进行判断即可得到答案,需要熟知平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.
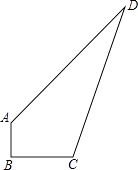
(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个相似三角形的周长比为3:4,那么它们的面积比是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某日傍晚,黄山的气温由上午的零下2℃下降了7℃,这天傍晚黄山的气温是℃.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线a、b、c在同一平面内,则下列说法错误的是( )
A. 如果a∥b,b∥c,那么a∥c
B. a⊥b,c⊥b,那么a∥c
C. 如果a与b相交,b与c相交,那么a与c一定相交
D. 如果a与b相交,b与c不相交,那么a与c一定相交
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列性质中,菱形具有而矩形不一定具有的是( )
A. 对角线互相平分 B. 对角线互相垂直 C. 对边平行且相等 D. 对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】6个人用35天完成了某项工程的
 ,如果再增加工作效率相同的8个人,那么完成这项工程,前后共用的天数是( )
,如果再增加工作效率相同的8个人,那么完成这项工程,前后共用的天数是( )
A. 30
B.40
C.60
D.65
相关试题

