【题目】如图,直径AE平分弦CD,交CD于点G,EF∥CD,交AD的延长线于F,AP⊥AC交CD的延长线于点P.
(1)求证:EF是⊙O的切线;
(2)若AC=2,PD= ![]() CD,求tan∠P的值.
CD,求tan∠P的值.
参考答案:
【答案】
(1)证明:∵直径AE平分弦CD,
∴AG⊥CD(垂径定理).
∵EF∥CD(已知),
∴∠AEF=∠AGD=90°.
∴EF是⊙O的切线.
(2)∵∠CAP=∠AGC=90°,∠ACG=∠PCA.
∴△CAG∽△CPA(AA).
∴AC2=CGCP(相似三角形的对应边成比例).
又∵PD= ![]() CD(已知),
CD(已知),
CG=GD,
∴CG= ![]() PC.而AC=2,
PC.而AC=2,
∴22= ![]() PCPC,∴PC2=12.
PCPC,∴PC2=12.
又∵AC⊥AP,∴AP2=PC2﹣AC2(勾股定理),
∴AP= ![]() .(13分)
.(13分)
∴tan∠P= ![]() .
.
【解析】(1)要证EF是⊙O的切线,只需证明∠AEF=90°即可.(2)首先利用相似三角形判定定理证明△CAG∽△CPA,利用性质:对应边成比例,得到AC2=CGCP,求得PC2=12,在直角三角形APC中利用勾股定理求得AP的长度,进而利用三角函数的定义求tan∠P的值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是AB的中点,点D是BC的中点,现给出下列等式:①CD=AC-DB,②CD=
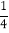 AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )
AB,③CD=AD-BC,④BD=2AD-AB.其中正确的等式编号是( )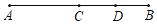
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在2019年1月份的月历表中,任意框出表中竖列上三个相邻的数(如图,如框出了10,17,24),则这三个数的和可能的是( )

A. 21B. 27C. 50D. 75
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题:
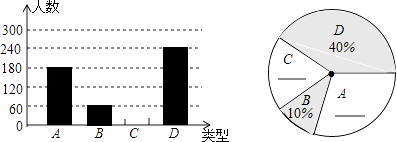
(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线l1:y=﹣x+n过点A(﹣1,3),双曲线C:y=
 (x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(x>0),过点B(1,2),动直线l2:y=kx﹣2k+2(常数k<0)恒过定点F.
(1)求直线l1 , 双曲线C的解析式,定点F的坐标;
(2)在双曲线C上取一点P(x,y),过P作x轴的平行线交直线l1于M,连接PF.求证:PF=PM.
(3)若动直线l2与双曲线C交于P1 , P2两点,连接OF交直线l1于点E,连接P1E,P2E,求证:EF平分∠P1EP2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿射线AB的方向平移2个单位到△DEF的位置,点A、B、C的对应点分别点D、E、F.
(1)直接写出图中与AD相等的线段.
(2)若AB=3,则AE=______.
(3)若∠ABC=75°,求∠CFE的度数.

相关试题

