【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
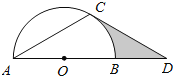
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
参考答案:
【答案】(1)见解析;(2)![]()
![]() .
.
【解析】
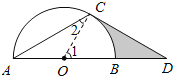
试题分析:(1)连接OC.只需证明∠OCD=90°.根据等腰三角形的性质即可证明;
(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积.
(1)证明:连接OC.
∵AC=CD,∠ACD=120°,
∴∠A=∠D=30°.
∵OA=OC,
∴∠2=∠A=30°.
∴∠OCD=180°﹣∠A﹣∠D﹣∠2=90°.即OC⊥CD,
∴CD是⊙O的切线.
(2)解:∵∠A=30°,
∴∠1=2∠A=60°.
∴S扇形BOC=![]() .
.
在Rt△OCD中,
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴图中阴影部分的面积为:![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地一天早晨的气温为﹣3℃,中午比早晨上升了7℃,夜间又比中午下降了8℃,则这天的夜间的气温是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为220的末位数字是( )
A.2 B.4 C.6 D.8
-
科目: 来源: 题型:
查看答案和解析>>【题目】使两个直角三角形全等的条件是( )
A. 一个锐角对应相等 B. 两个锐角对应相等
C. 一条边对应相等 D. 斜边及一条直角边对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】在小学,我们已经初步了解到,正方形的每个角都是90°,每条边都相等.如图,在正方形ABCD外侧作直线AQ,且∠QAD=30°,点D关于直线AQ的对称点为E,连接DE、BE,DE交AQ于点G,BE交AQ于点F.
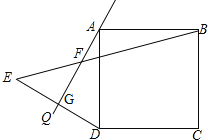
(1)求∠ABE的度数;
(2)若AB=6,求FG的长.
-
科目: 来源: 题型:
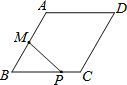
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A.
 B.
B. C.
C.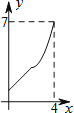 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在对代数式2x2+ax﹣y+6﹣(bx2+3x﹣5y+1)化简后,没有含x的项,请求出代数式(a﹣b)2的值.
相关试题

