【题目】如图,E、F是四边形ABCD的对角线AC上两点,AE=CF,DF∥BE,DF=BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AC平分∠BAD,求证:ABCD为菱形.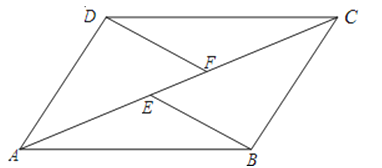
参考答案:
【答案】证明:(1)∵DF∥BE,
∴∠DFA=∠CEB,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
在△ADF和△CBE中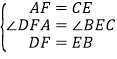 ,
,
∴△ADF≌△CBE(SAS),
∴AD=CB,∠DAC=∠ACB,
∴AD∥CB,
∴四边形ABCD是平行四边形;
(2)∵AC平分∠BAD,
∴∠DAC=∠BAC,
∴∠BAC=∠ACB,
∴AB=BC,
∴ABCD为菱形.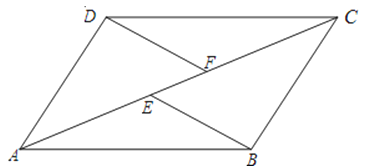
【解析】(1)首先证明△ADF≌△CBE,根据全等三角形的性质可得AD=CB,∠DAC=∠ACB,进而可得证明AD∥CB,根据一组对边平行且等的四边形是平行四边形可得四边形ABCD是平行四边形;
(2)首先根据角平分线的性质可得∠DAC=∠BAC,进而可得出AB=BC,再根据一组邻边相等的平行四边形是菱形可得结论.
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若AB∥CD,AB∥EF,则______ ∥ ______ ,理由是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,直线L垂直分线段AC,垂足为O,直线L分别于线段AD,CB的延长线交于点E,F,证明四边形AFCE是菱形.
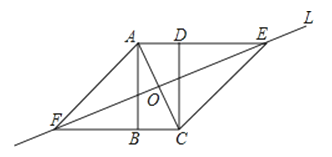
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一元二次方程x2-6x+a =0有一个根为2,则另一根为_______.
-
科目: 来源: 题型:
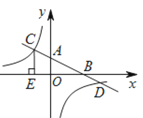
查看答案和解析>>【题目】如图,在平面直角坐标系xoy中,一次函数y1=ax+b的图象分别与x,y轴交于点B,A,与反比例函数y2=
 的图象交于点C,D,CE⊥x轴于点E,tan∠ABO=
的图象交于点C,D,CE⊥x轴于点E,tan∠ABO= ,OB=4,OE=2.
,OB=4,OE=2.(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出当x<0且y1<y2时x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为丰富学生课外活动,某校积极开展社团活动,学生可根据自己的爱好选择一项,已知该校开设的体育社团有:A:篮球,B:排球C:足球;D:羽毛球,E:乒乓球.李老师对某年级同学选择体育社团情况进行调查统计,制成了两幅不完整的统计图(如图),则以下结论不正确的是( )
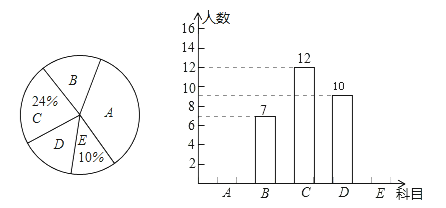
A.选科目E的有5人
B.选科目D的扇形圆心角是72°
C.选科目A的人数占体育社团人数的一半
D.选科目B的扇形圆心角比选科目D的扇形圆心角的度数少21.6° -
科目: 来源: 题型:
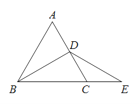
查看答案和解析>>【题目】如图,△ABC是等边三角形,点D是AC的中点,延长BC到E,使CE=CD.
(1)用尺规作图的方法,过点D作DM⊥BE,垂足为M(不写作法,只保留作图痕迹);
(2)若AB=2,求EM的长.
相关试题

