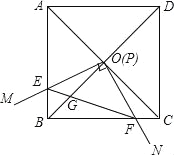
【题目】如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1)EF=![]() OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=
OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=![]() OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=
OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;(5)OGBD=AE2+CF2.
;(5)OGBD=AE2+CF2.
参考答案:
【答案】(1),(2),(3),(5).
【解析】
试题分析:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
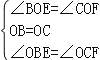 ,
,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=![]() OE;故正确;
OE;故正确;
(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=![]() S正方形ABCD,
S正方形ABCD,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
(3)∴BE+BF=BF+CF=BC=![]() OA;故正确;
OA;故正确;
(4)过点O作OH⊥BC,
∵BC=1,
∴OH=![]() BC=
BC=![]() ,
,
设AE=x,则BE=CF=1﹣x,BF=x,
∴S△BEF+S△COF=![]() BEBF+
BEBF+![]() CFOH=
CFOH=![]() x(1﹣x)+
x(1﹣x)+![]() (1﹣x)×
(1﹣x)×![]() =﹣
=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵a=﹣![]() <0,
<0,
∴当x=![]() 时,S△BEF+S△COF最大;
时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=![]() ;故错误;
;故错误;
(5)∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OGOB=OE2,
∵OB=![]() BD,OE=
BD,OE=![]() EF,
EF,
∴OGBD=EF2,
∵在△BEF中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
∴OGBD=AE2+CF2.故正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=ax+b的图象经过点(1,2),点(﹣1,6),且与x轴交于点B,与y轴交于点A.
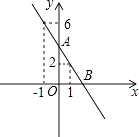
(1)求出这个一次函数的解析式;
(2)求出一次函数图象与两坐标轴围成的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:
 ≈1.414,
≈1.414, ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE,若∠E=50°,求∠BAO的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,历经一年半的调查研究,北京PM2.5源解析已经通过专家论证.各种调查显示,机动车成为PM2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天就要向大气里排放0.035千克污染物.以下是相关的统计图表:
2014年北京市全年空气质量等级天数统计表空气质量等级
优
良
轻度污染
中度污染
重度污染
严重污染
天数(天)
41
135
84
47
45
13
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?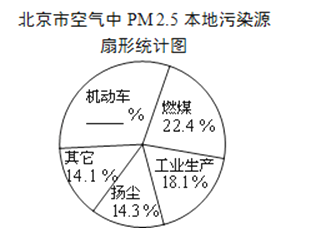
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如表(单位:秒):此题图片显示不全

一
二
三
四
五
六
七
八
九
十
甲种电子钟
1
﹣3
﹣4
4
2
﹣2
2
﹣1
﹣1
2
乙种电子钟
4
﹣3
﹣1
2
﹣2
1
﹣2
2
﹣2
1
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级举行“做创新型青年”的演讲比赛,派了两位老师去学校附近的超市购买笔记本作为奖品.经过了解得知,该超市的A、B两种笔记本的价格分别是12元和8元,他们准备购买这两种笔记本共30本.
(1)如果他们计划用300元购买奖品,那么能买这两种笔记本各多少本?
(2)两位老师根据演讲比赛的设奖情况,决定所购买的A种笔记本的数量不少于B种笔记本数量的
 ,如果设他们买A种笔记本n本,买这两种笔记本共花费W元.
,如果设他们买A种笔记本n本,买这两种笔记本共花费W元.①请写出W (元)关于n (本)的函数关系式,并求出自变量n的取值范围;
②请你帮他们计算,购买这两种笔记本各多少时,花费最少,此时花费是多少元?
相关试题

