【题目】在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则满足下列条件但不是直角三角形的是( )
A.a2-c2=b2B.a=n2-1, b=2n, c=n2+1 ( n>1)
C.∠A:∠B:∠C = 3:4:5D.∠A=∠B =![]() ∠C
∠C
参考答案:
【答案】C
【解析】
根据直角三角形的判定方法,利用角,边的关系从而来判定是否是直角三角形.
选项A,![]() ,变形为
,变形为![]() ,
,![]() ,即△ABC是直角三角形;
,即△ABC是直角三角形;
选项B,![]() ,
,![]() ,即△ABC是直角三角形;
,即△ABC是直角三角形;
选项C,∵∠A:∠B:∠C=3:4:5,∠A+∠B+∠C=180°,∴∠A=45°,∠B=60°,∠C=75°,即△ABC不是直角三角形,故本选项错误;
选项D,∠A=∠B =![]() ∠C,∠A+∠B+∠C=180°,即2∠C=180°,解得∠C=90°,即△ABC是直角三角形.
∠C,∠A+∠B+∠C=180°,即2∠C=180°,解得∠C=90°,即△ABC是直角三角形.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点A对应的数为a,点B对应的数为b,且多项式6x3y-2xy+5的二次项系数为a,常数项为b
(1) 直接写出:a=__________,b=_________
(2) 数轴上点P对应的数为x,若PA+PB=20,求x的值
(3) 若点M从点A出发,以每秒1个单位长度的速度沿数轴向右移动;同时点N从点B出发,以每秒2个单位长度的速度沿数轴向左移动,到达A点后立即返回并向右继续移动,求经过多少秒后,M、N两点相距1个单位长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )

A. 20 B. 25 C. 30 D. 35
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3),B(﹣3,1),C(﹣1,3).
(1)请按下列要求画图:
①平移△ABC,使点A的对应点A1的坐标为(﹣4,﹣3),请画出平移后的△A1B1C1;
②△A2B2C2与△ABC关于原点O中心对称,画出△A2B2C2.
(2)若将△A1B1C1绕点M旋转可得到△A2B2C2,请直接写出旋转中心M点的坐标 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】填写下列证明过程中的推理根据:
已知:如图所示,AC,BD相交于O,DF平分∠CDO与AC相交于F,BE平分于∠ABO与AC相交于E,∠A=∠C.求证:∠1=∠2.
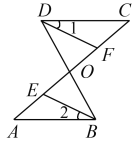
证明:∵∠A=∠C(________),
∴AB∥CD (__________________________________),
∴∠ABO=∠CDO (__________________________________),
又∵∠1=
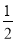 CDO,∠2=
CDO,∠2=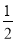 ∠ABO (__________________________________),
∠ABO (__________________________________),∴∠1=∠2(____________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a+b=2,则称a与b是关于1的平衡数.
(1)3与 是关于1的平衡数,5﹣
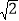 与 是关于1的平衡数;
与 是关于1的平衡数;(2)若(m+
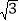 )×(1﹣
)×(1﹣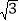 )=﹣5+3
)=﹣5+3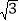 ,判断m+
,判断m+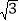 与5﹣
与5﹣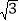 是否是关于1的平衡数,并说明理由.
是否是关于1的平衡数,并说明理由.
相关试题

