【题目】“十一”期间沈阳世博园(10月1日)的进园人数为![]() 万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
万人,以后的6天里每天的进园人数变化如下表(正数表示比前一天多的人数负数表示比前一天少的人数,单位:万人)
日期 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 |
|
|
|
|
|
|
(1)10月2日的进园人数是多少?
(2)10月1日-10月7日这7天内的进园人数最多的是哪天?最少的是哪天?它们相差多少?
参考答案:
【答案】(1)![]() 万人;(2)10月2日最多,10月5日最少,相差
万人;(2)10月2日最多,10月5日最少,相差![]() 万人.
万人.
【解析】
(1)根据题意,利用有理数加法运算法则计算出答案即可;
(2)根据题意得出各天之中进园的人数,然后进一步加以比较即可.
(1)根据题意可得:![]() (万人),
(万人),
答:10月2日的进园人数是![]() 万人;
万人;
(2)根据题意可得各天的进园人数为:
10月1日:20.3万人;10月2日:![]() (万人)
(万人)
10月3日:![]() (万人);10月4日:
(万人);10月4日:![]() (万人);
(万人);
10月5日:![]() (万人);10月6日:
(万人);10月6日:![]() (万人);
(万人);
10月7日:![]() (万人)
(万人)
∴10月2日人最多,10月5日人最少,
二者相差![]() (万人).
(万人).
答:10月2日人最多,10月5日人最少,相差![]() 万人.
万人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一长
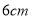 ,宽
,宽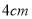 的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转
的长方形纸板,现要求以其一组对边中点所在直线为轴,旋转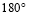 ,得到一个几何体(结果保留
,得到一个几何体(结果保留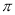 );
);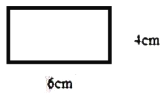
(1)写出该几何体的名称__________;
(2)所构造的圆柱体的侧面积__________;
(3)求所构造的圆柱体的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
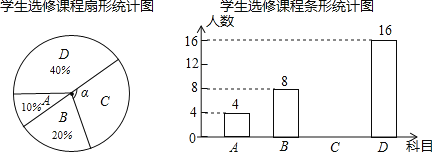
(1)本次调查的学生共有多少人?扇形统计图中∠α的度数是多少?
(2)请把条形统计图补充完整;
(3)学校为举办2018年度校园文化艺术节,决定从A.书法;B.绘画;C.乐器;D.舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或树状图求出选中书法与乐器组合在一起的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的
 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代对于利用方程解决实际问题早有研究,《九章算术》中提到这么一道“以绳测井”的题:以绳测井,若将绳三折测之,绳多四尺:若将绳四折测之,绳多一尺.绳长、井深各几何?
这道题大致意思是:用绳子测量水井深度,如果将绳子折成三等份,那么每等份井外余绳四尺:如果将绳子折成四等份,那么每等份井外余绳一尺.问绳长和井深各多少尺?若设井深为x尺,则求解井深的方程正确的是( )
A.3(x+4)=4(x+1)B.3x+4=4x+1
C.
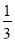 x+4=
x+4=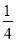 x+1D.
x+1D.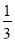 x﹣4=
x﹣4=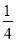 x﹣1
x﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了保障人畜饮水安全,某县急需饮水设备12台,现有甲、乙两种设备可供选择,已知购买1台甲种设备和2台乙两种设备共需10000元,购买3台甲种设备和1台乙两种设备共需15000元,且甲种设备的安装及运输费用为600元/台,乙种设备的安装及运输费用为800元/台.
(1)购买1台甲、乙两种设备各需多少元?
(2)若购买的费用不超过40000元,安装及运输费用不超过9200元,则有几种购买方案?
-
科目: 来源: 题型:
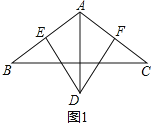
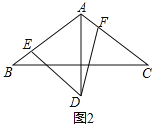
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=120,AD⊥BC,且AD=AB.
(1)如图1,DE⊥AB,DF⊥AC,垂足分别为点E,F,求证:AE+AF=AD
(2)如图2,如果∠EDF=60,且∠EDF两边分别交边AB,AC于点E,F,那么线段AE,AF,AD之间有怎样的数量关系?并给出证明.
相关试题

